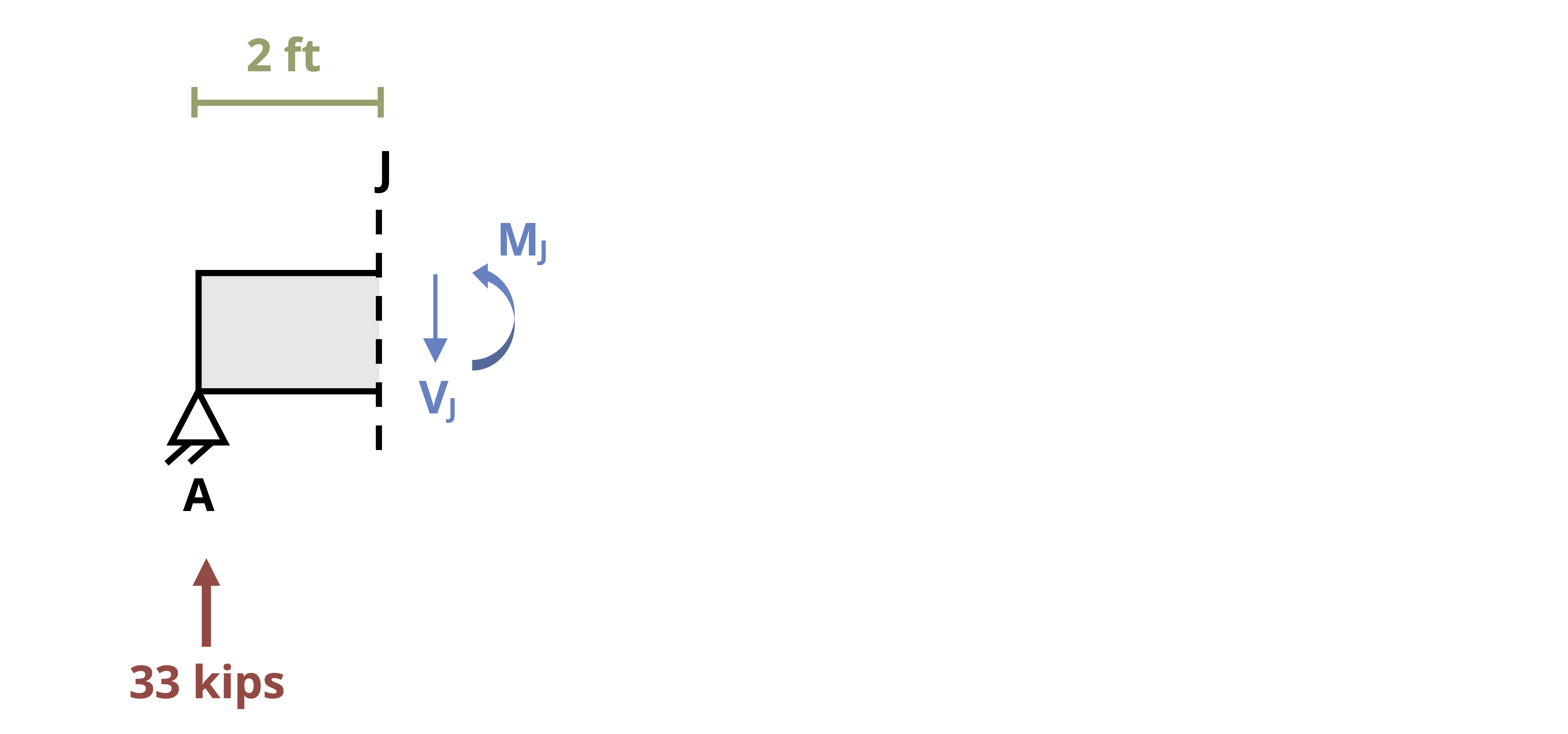7  Beams

NoteLearning Objectives
  • Apply equilibrium methods to determine internal shear forces and bending moments equations, and specific values in beams
  • Draw the shear and bending moment diagrams using integration and graphical methods
The left image shows a construction site with large steel or timber beams casting angular shadows onto a gravel surface, viewed from a low angle beneath the structure. The center image depicts a close-up of a wooden roof truss system with diagonal and vertical members joined by metal plates, set against a clear blue sky. The right image features the iconic Fallingwater house by Frank Lloyd Wright, with cantilevered concrete balconies projecting over a waterfall, surrounded by forest.
Figure 7.1: Examples of structural beams

Beams are structural members that support loads along their length. Typically these loads are perpendicular to the axis of the beam and cause only shear and bending moments. Figure 7.1 shows some examples.

As evident in previous chapters, internal forces and moments are crucial to calculating stresses and deflections. The same is true for finding stresses and deflections in beams. Due to the nature of the loadings and constraints of beams, finding internal forces requires new methods in statics. This chapter describes these methods for finding a beam’s internal shear force and bending moments.

Section 7.1 reviews how to find the internal shear force and bending moments at a specific point in a beam using equilibrium. Section 7.2 discusses relationships between the applied load, the internal shear force, and the internal bending moment.

Then follows a discussion of a more general approach to visualizing the internal shear force and bending moment at different points in a beam using diagrams of these. Section 7.3 explores how to draw these diagrams using an equilibrium method. Then Section 7.4 provides an alternative graphical method for drawing these diagrams.

Before presenting methods for finding internal shear and moments of beams, we need to establish a sign convention to provide consistency and act as a guide to interpreting our results. Note that anytime you start a new project or subject, you should ensure that a sign convention is established.

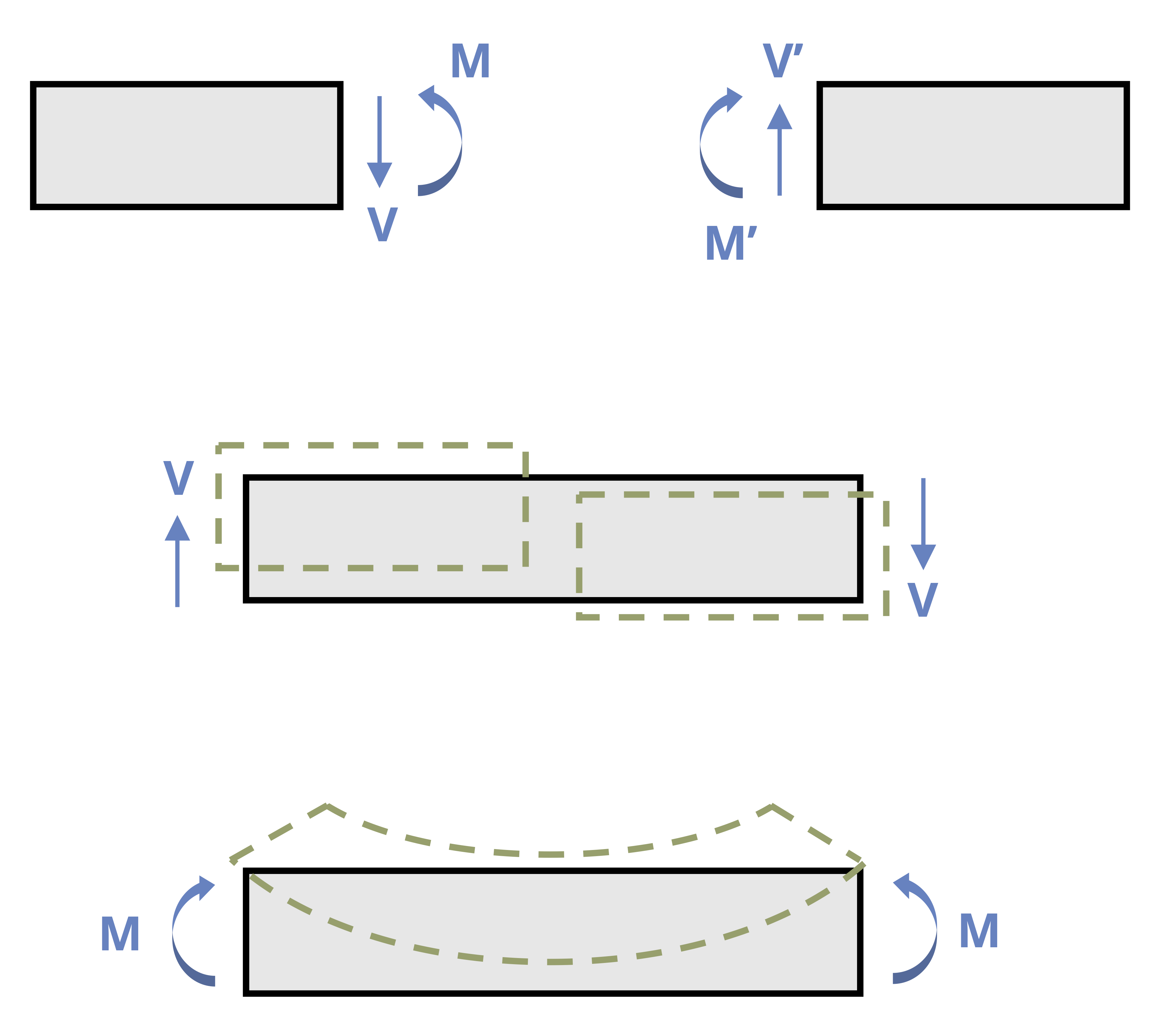
Internal shear and bending moment effects on a beam. The top row shows two rectangular segments with vertical shear forces (V and V′) and internal moments (M and M′) acting in opposing directions. The middle image shows a rectangular beam with dashed outlines on both sides indicating deformation due to internal shear forces, with vertical arrows showing opposing shear (V) at the cut sections. The bottom image shows the same beam with a parabolic dashed outline indicating displacement due to bending, with clockwise and counterclockwise internal moments (M) applied at both ends.
Figure 7.2: Positive sign convention for internal shear force (V) and bending moment (M)

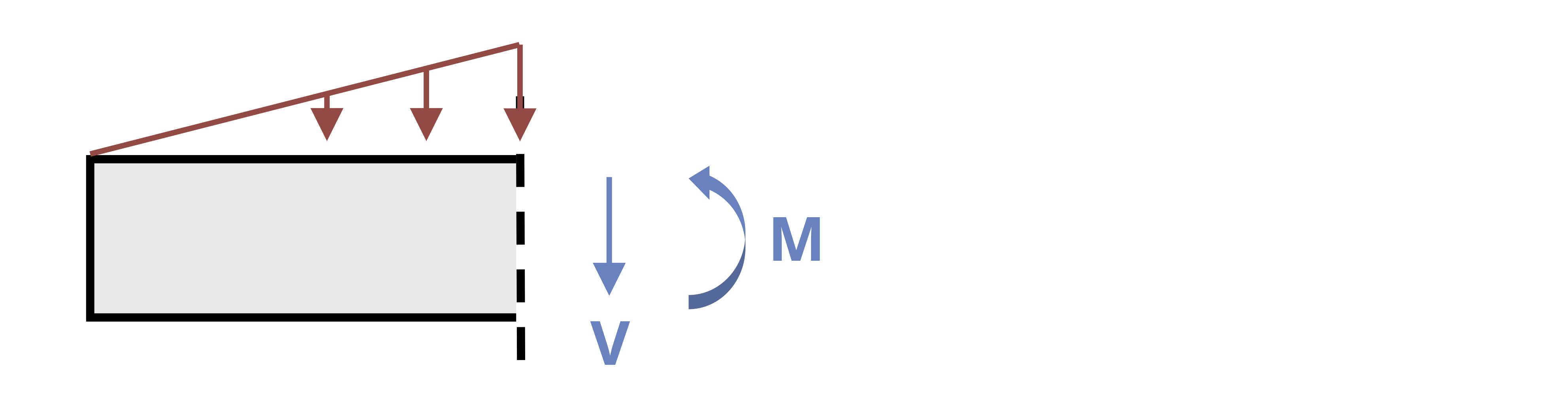
For the purposes of this book, the shear is positive when the external forces shear off as depicted in Figure 7.2. Another way to think about it is that a positive shear is when the internal shear forces cause a clockwise rotation of the beam segment.

The bending moment is positive when the external forces bend the beam in a concave up shape as indicated in Figure 7.2. This causes the top fibers of the beam to be in compression while the bottom fibers are in tension.

7.1 Internal Shear Force and Bending Moment by Equilibrium

Click to expand

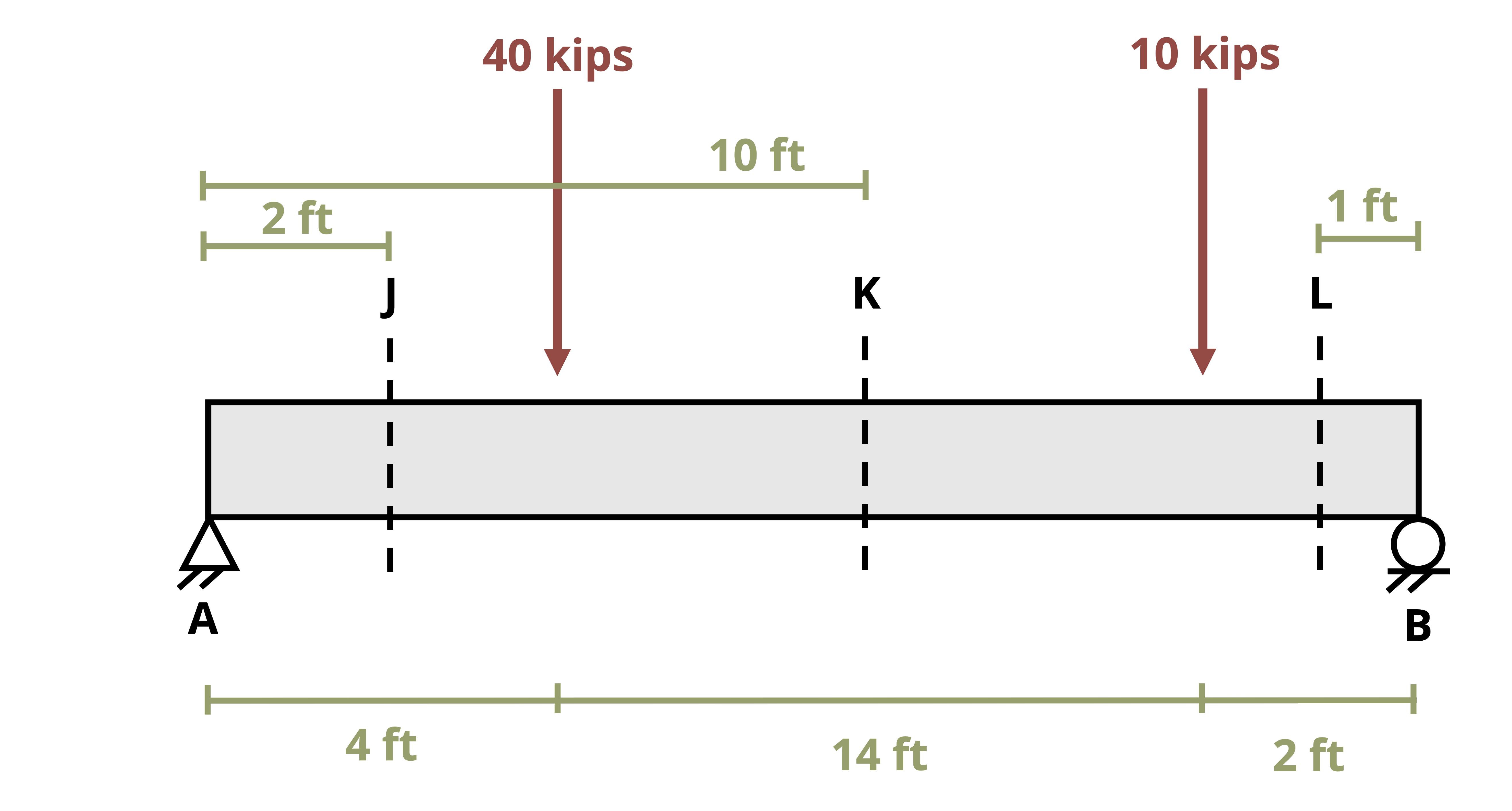
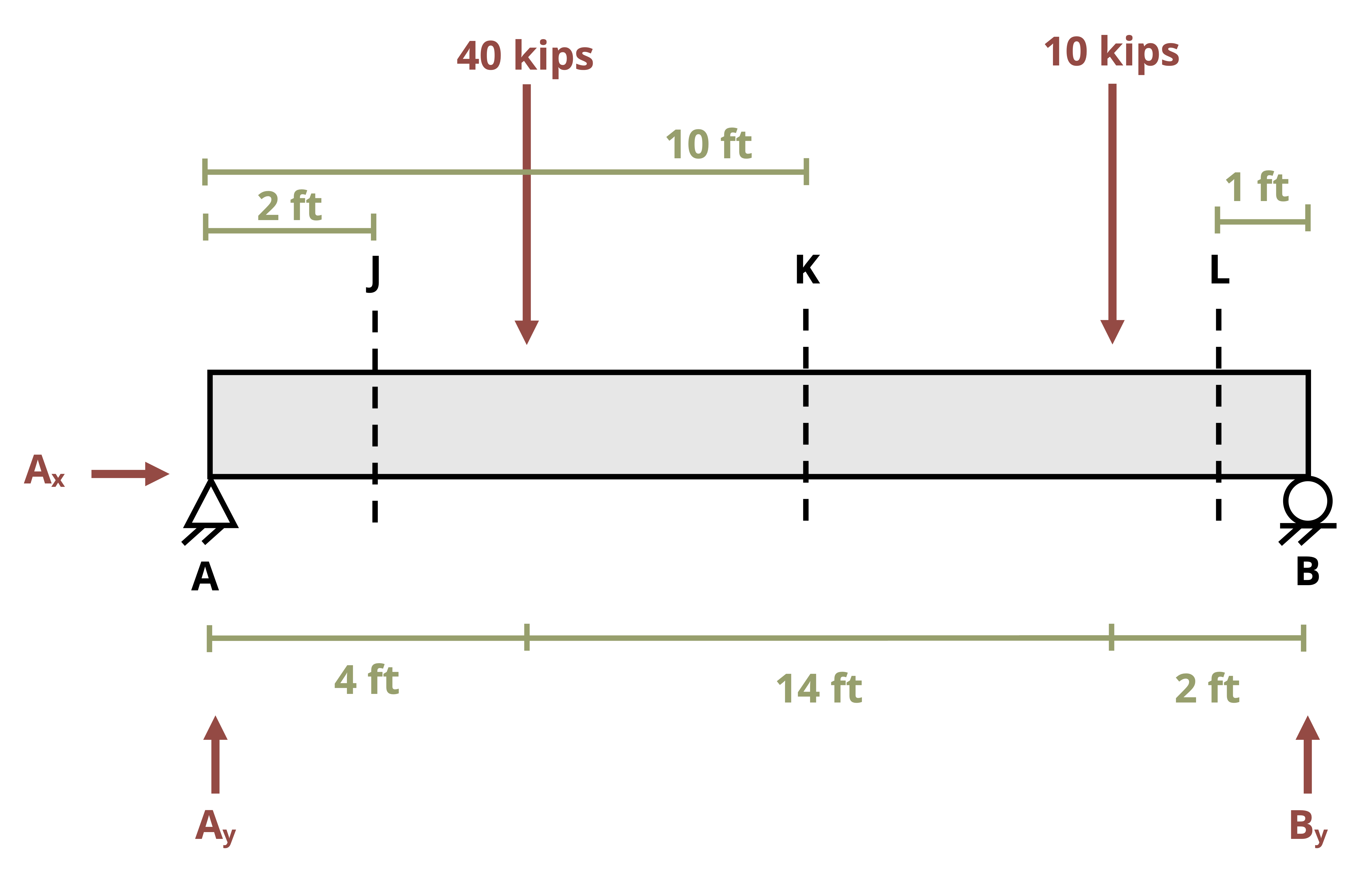
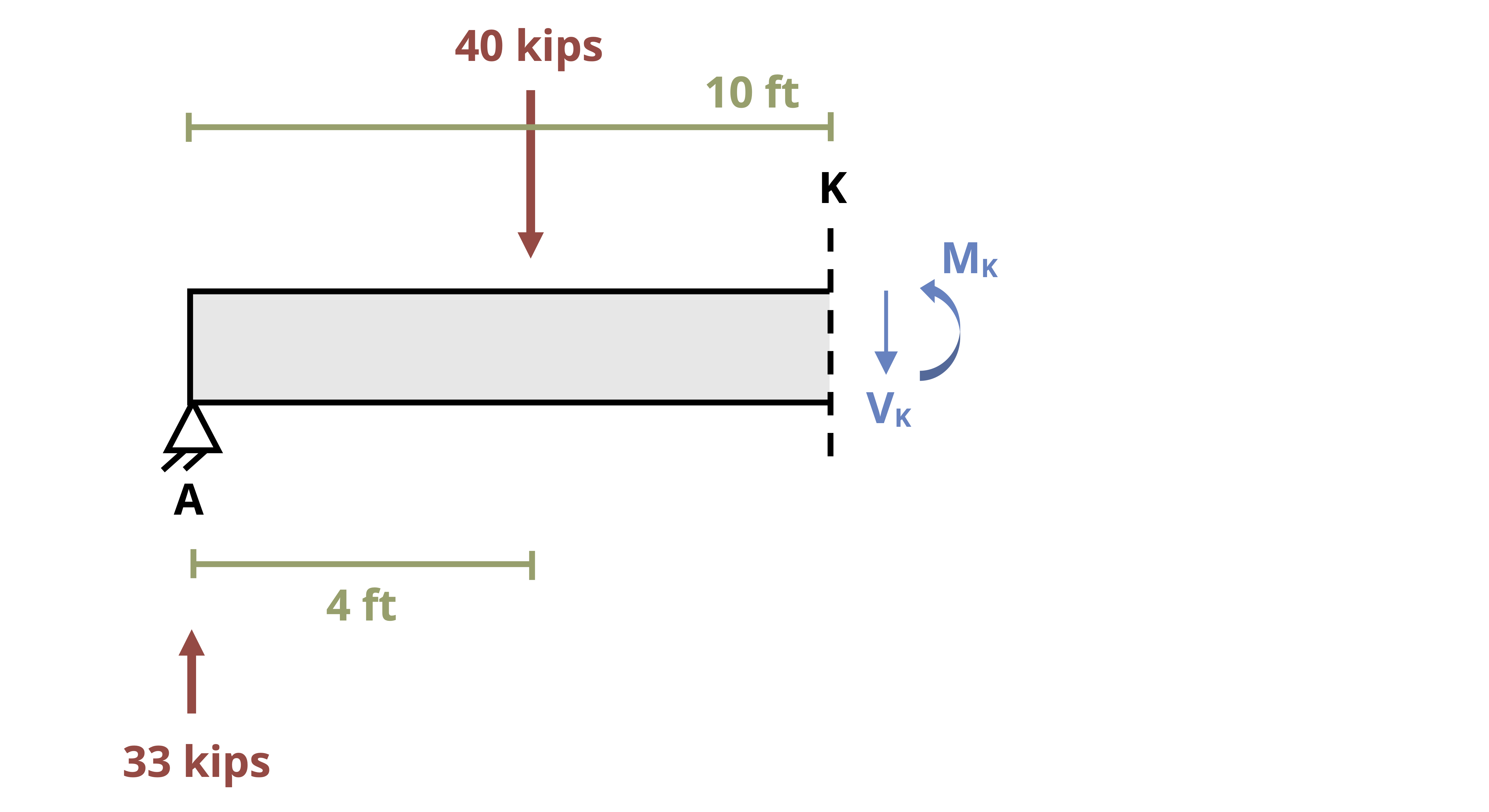
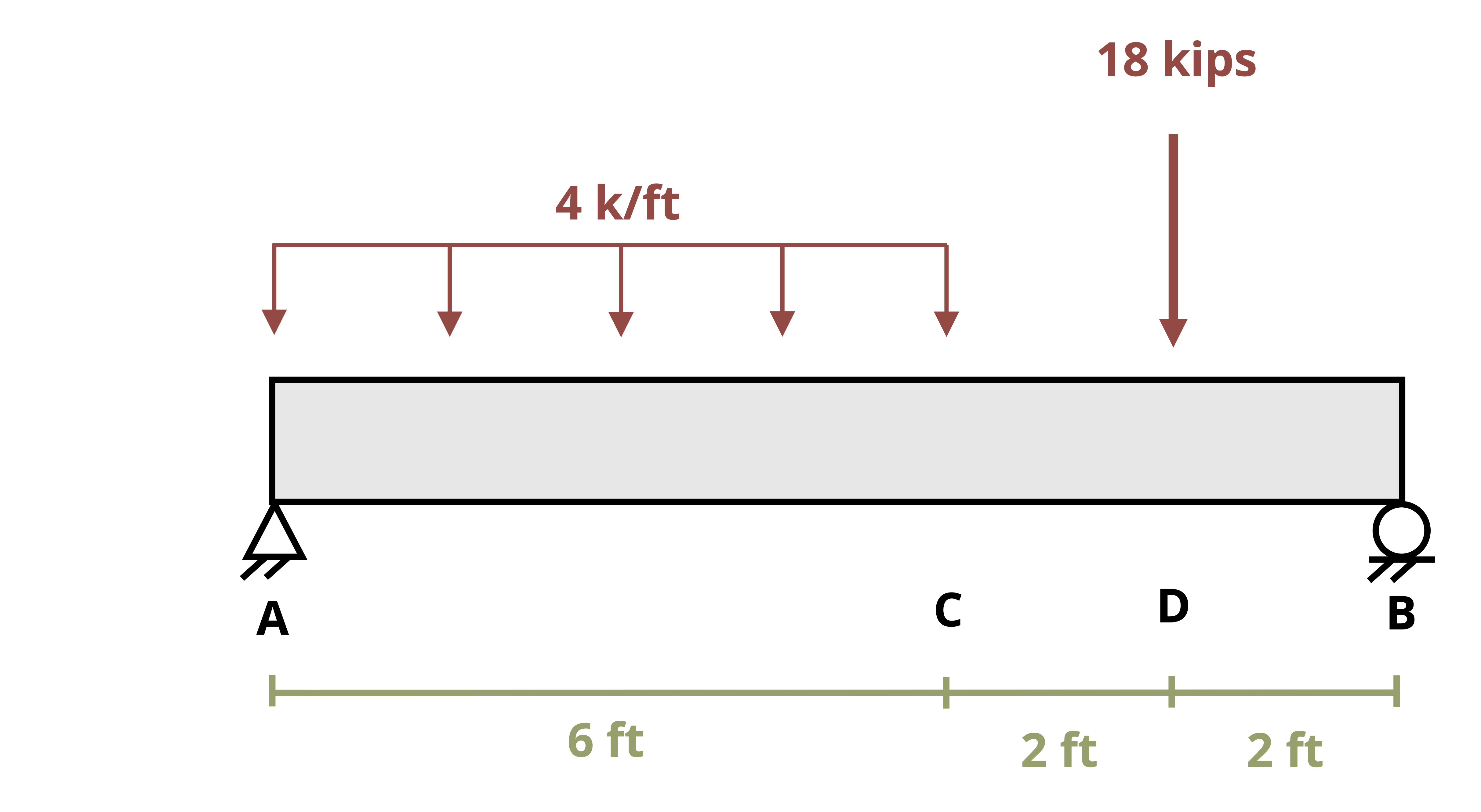
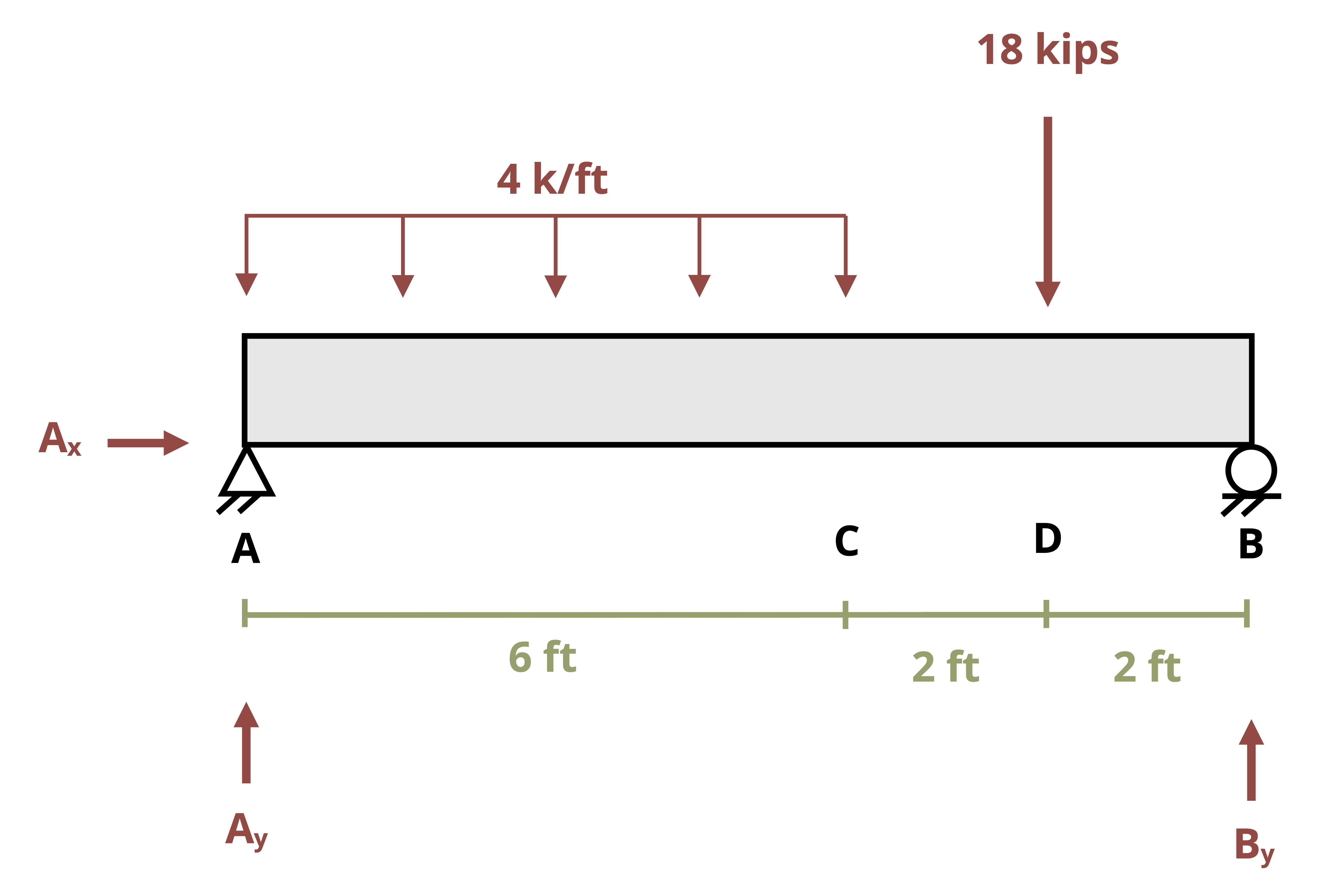
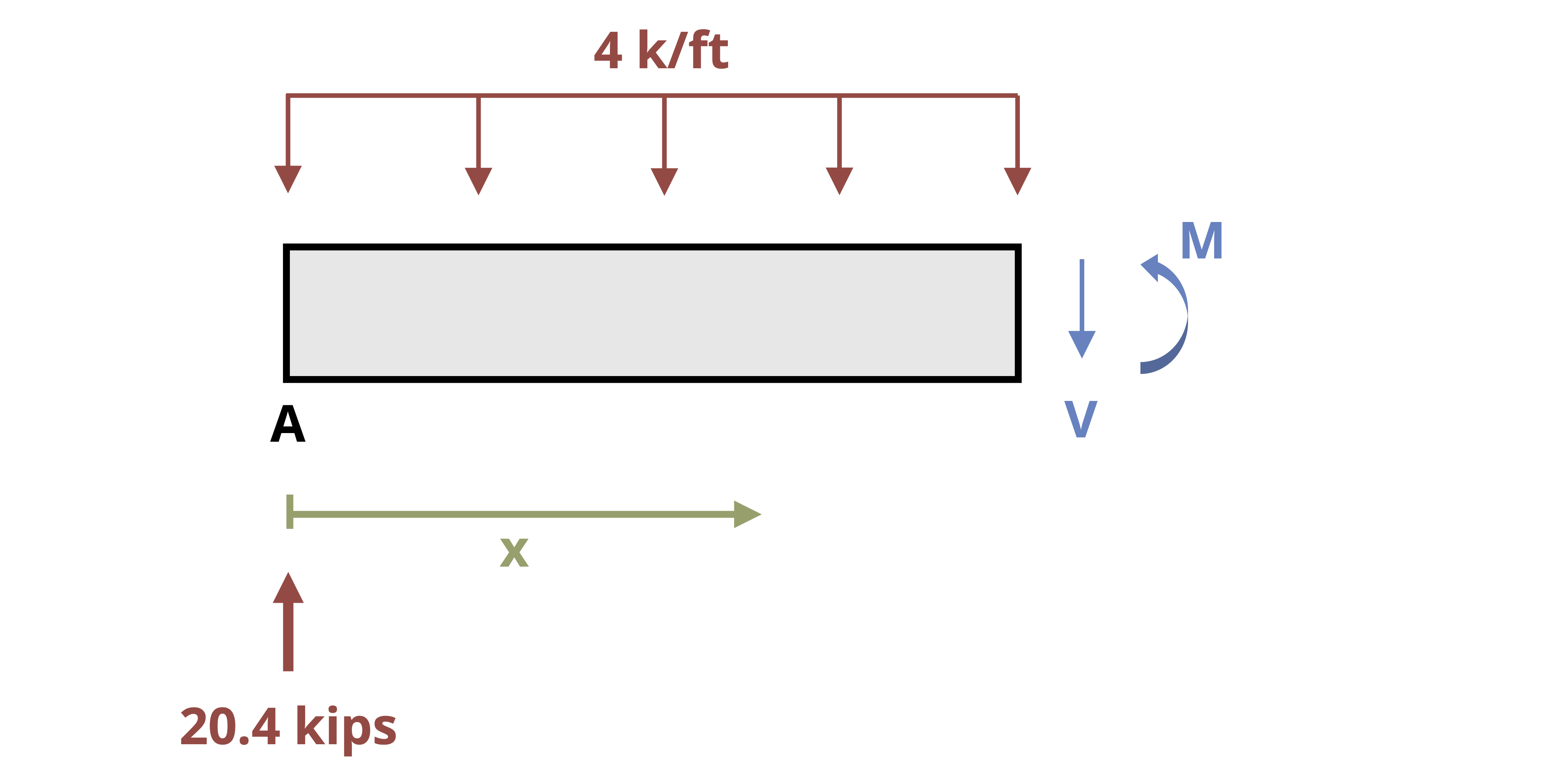
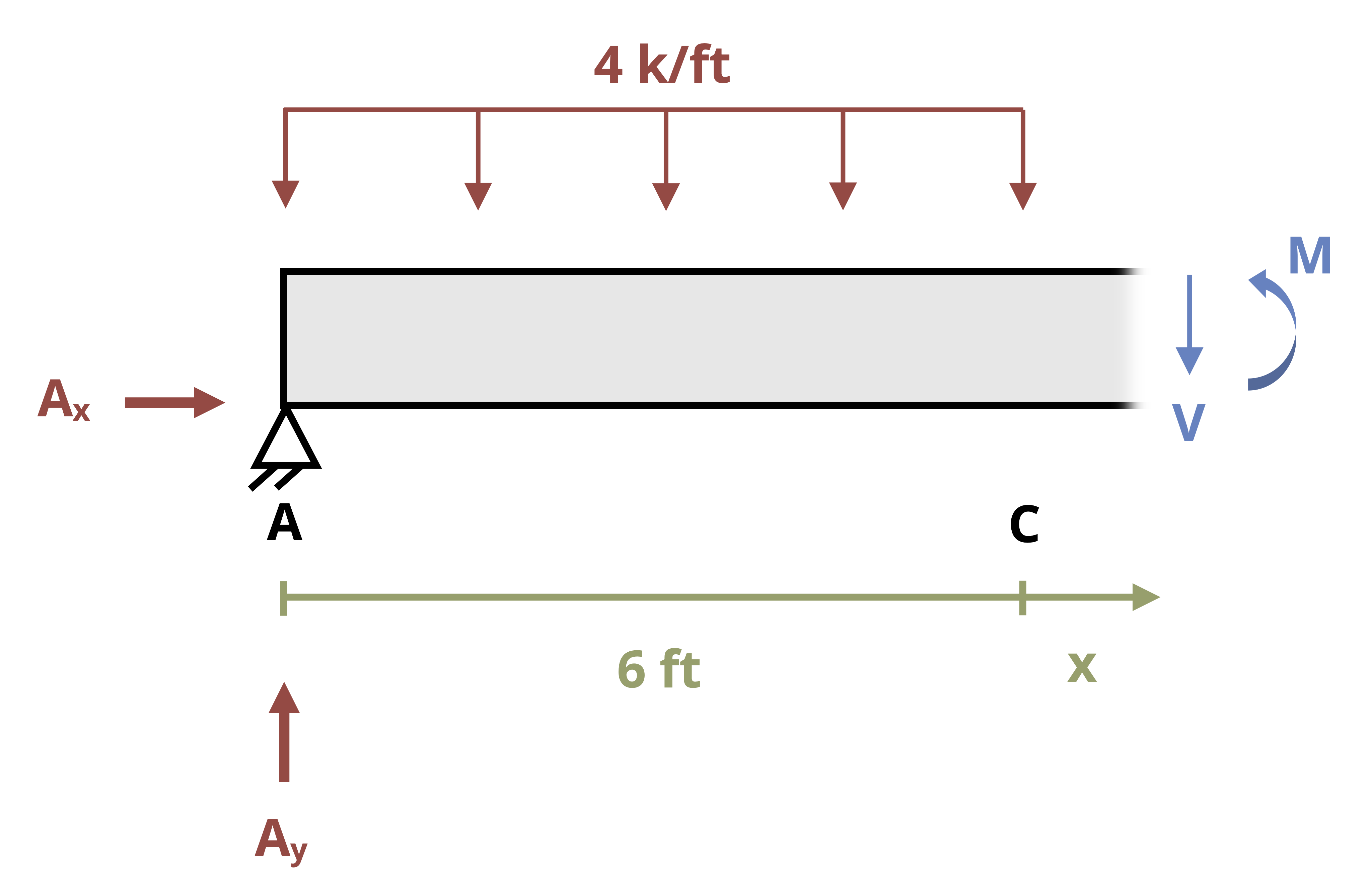
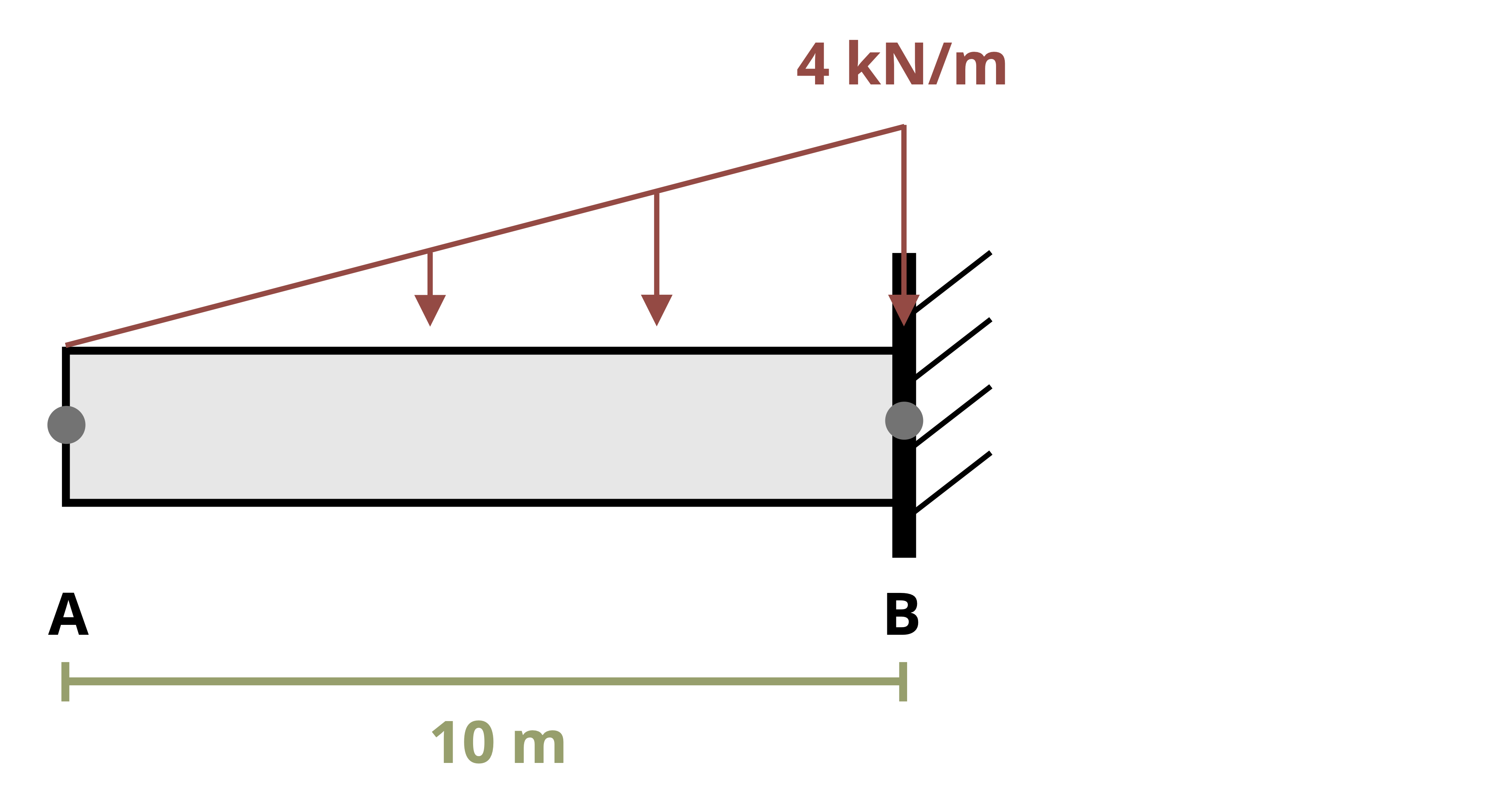
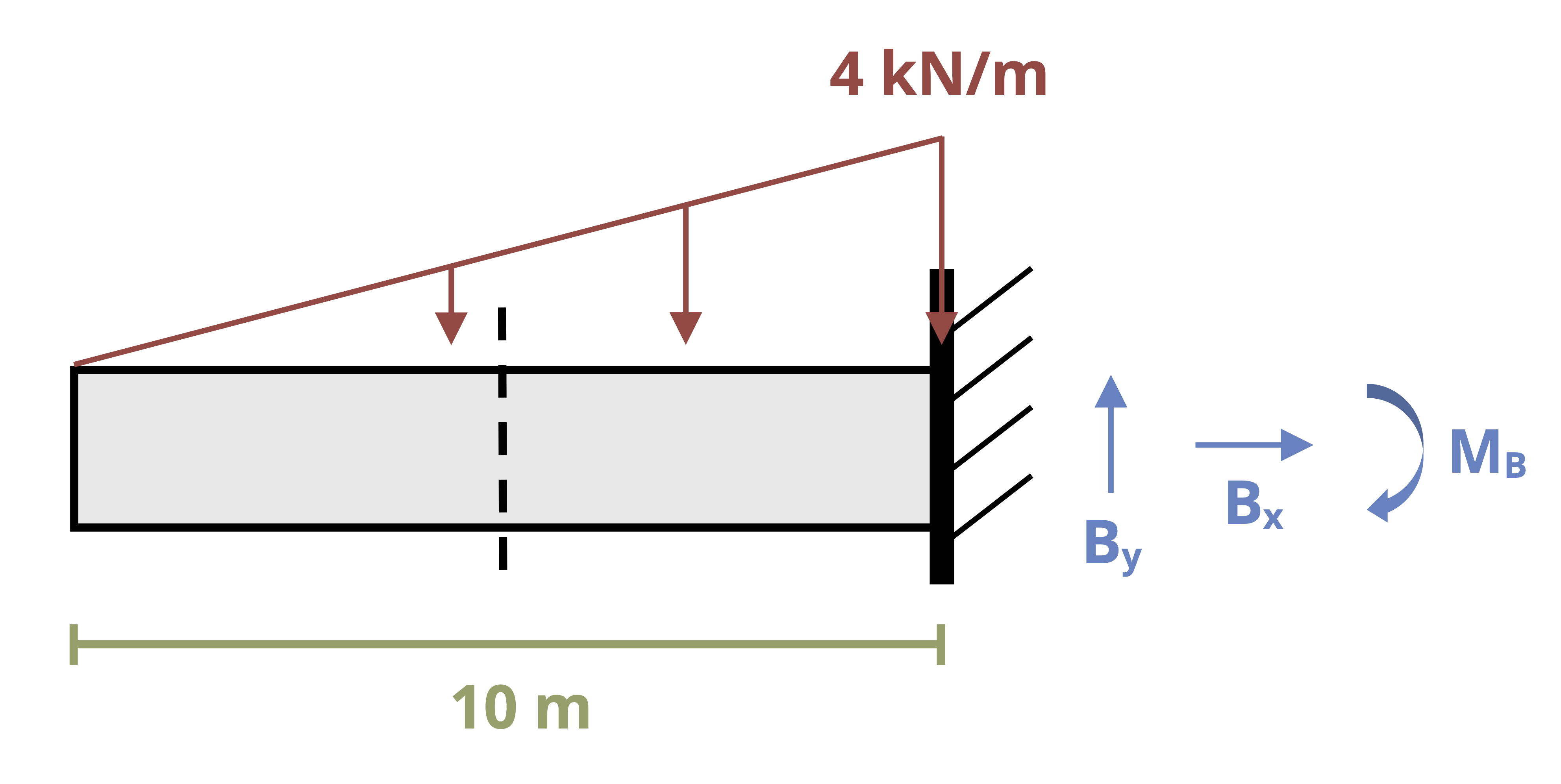
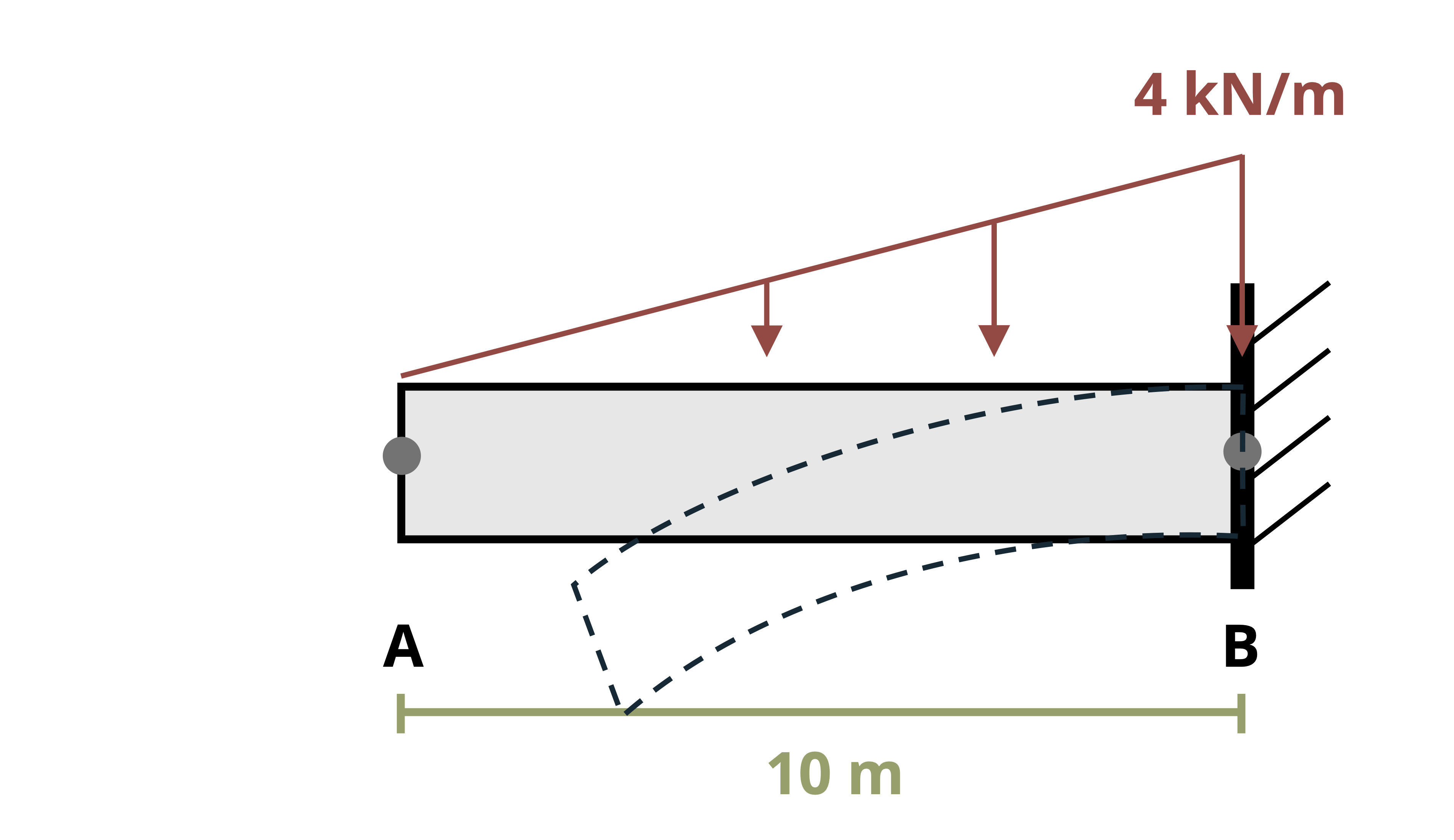
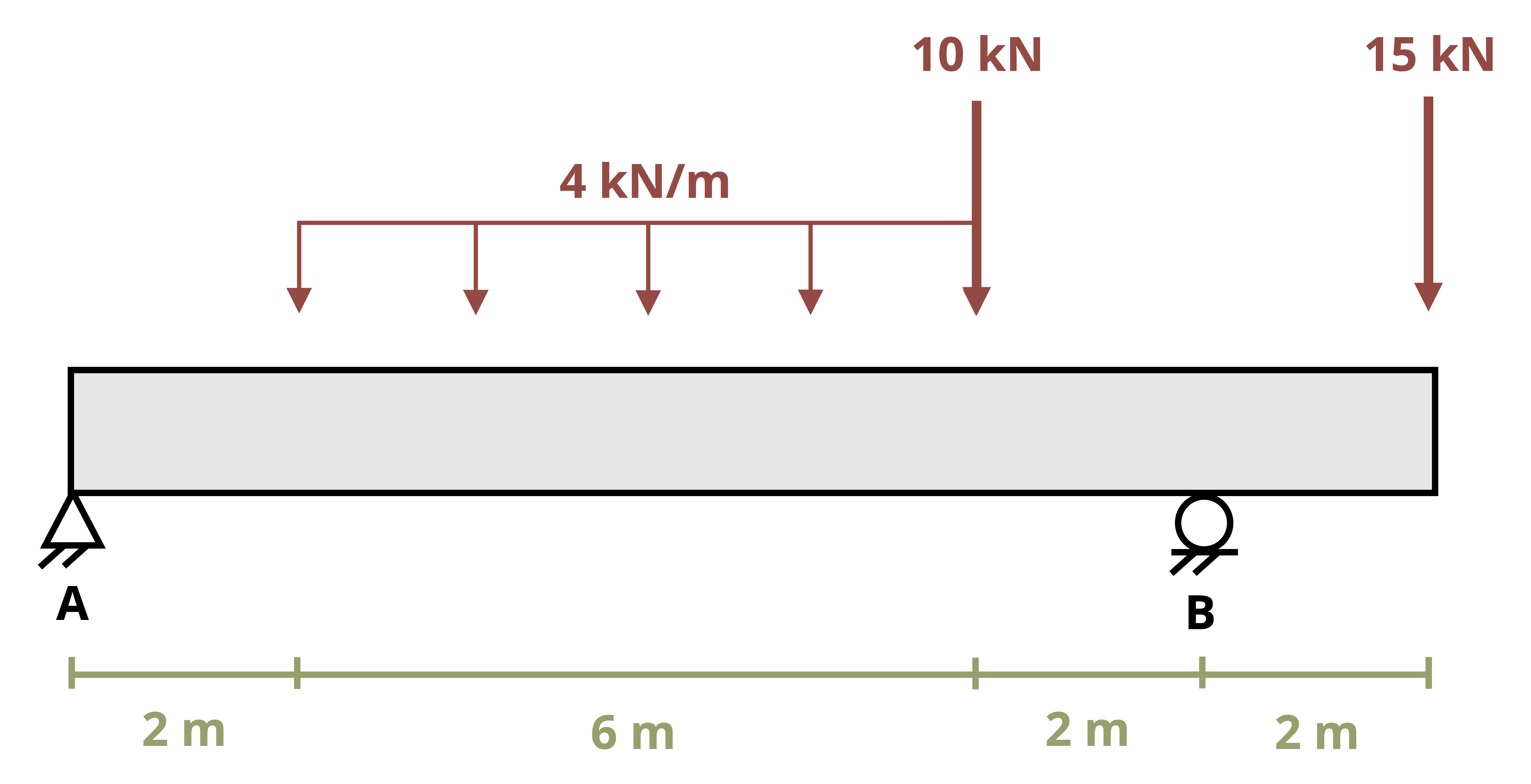
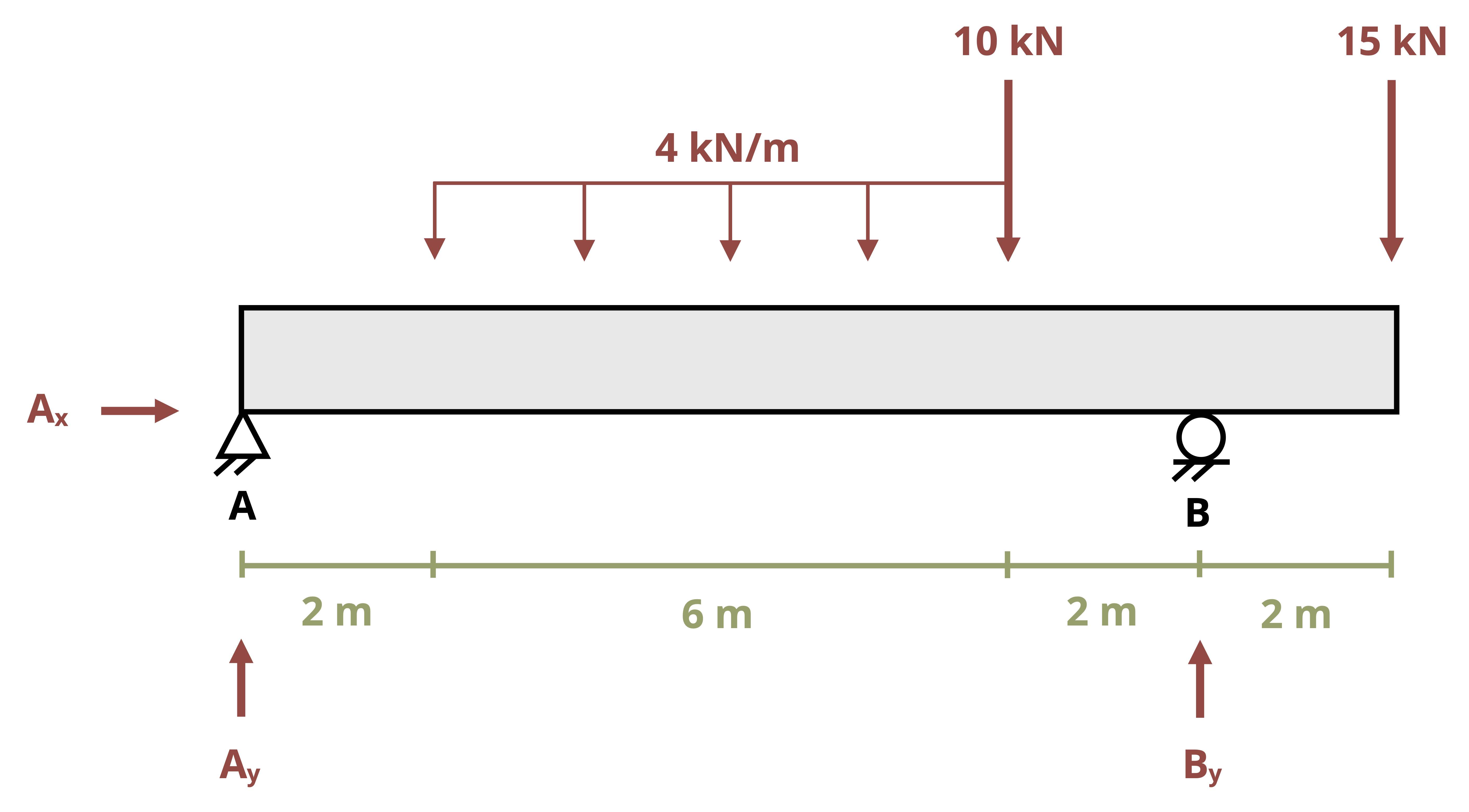
One way to find internal shear and bending forces is to cut sections and analyze the free body diagrams (FBDs), as we did in previous chapters of this book. The first step for a statically determinate beam—one where all forces can be found using only equilibrium equations—is to find the external reactions. To determine the internal forces at any point along the beam, we cut the section at that point and draw the FBD from that point to one end of the beam. We’ll include the internal shear force, V, and internal bending moment, M, at the cut section and then use equilibrium equations to solve for those internal loads. This process is demonstrated in Example 7.1.

Example 7.1  

Find the internal shear and bending moment at points J, K, and L in the pictured beam.

A horizontal beam AB is supported by a pin at point A on the far left and a roller at point B on the far right. The total length of the beam is 20 feet. Vertical downward forces are applied at two points: a 40 kip force is located 4 feet to the right of point A, and a 10 kip force is located 2 feet to the left of point B. Dashed lines mark points J, K, and L: J is 2 feet right of A, K is 10 feet right of A, and L is 1 foot left of B.

The first step is to find the external reactions at the supports A and B.

A horizontal beam AB is 20 feet long, supported by a pin at point A on the far left and a roller at point B on the far right. Reaction forces are shown: A sub x (horizontal, rightward) and A sub y (vertical, upward) at point A, and B sub y (vertical, upward) at point B. Two vertical downward forces are applied: a 40 kip force located 4 feet to the right of point A, and a 10 kip force located 2 feet to the left of point B. The beam is divided by vertical dashed lines at three points: J is 2 feet from A, K is 10 feet from A, and L is 1 foot from B.

\[ \begin{aligned} & \sum F_x=A_x=0 \\ & \sum M_A=-40{~kips}*4{~ft}-10{~kips}*18{~ft}+B_y*20{~ft}=0 \quad\rightarrow\quad B_y=17{~kips} \\ & \sum F_y=A_y-40-10+17=0 \quad\rightarrow\quad A_y=33{~kips} \end{aligned} \]

Next we draw an FBD of the right end of the beam from point A to J by cutting the beam at section J. The internal forces VJ and MJ are placed at the point of the cut using the positive sign convention. Note that you can assume the direction of these forces since the statics will work out the correct direction.

Section J

To find the internal shear, sum forces in the y direction. To find the internal moment, sum moments at point J.

A segment of a beam between point A and point J is shown. Point A on the left end is a pinned support with an upward vertical reaction force labeled 33 kips. The segment extends 2 feet horizontally to the right from point A to point J, where a vertical dashed line is drawn. At point J, a downward internal shear force V sub J and a counterclockwise internal moment M sub J are shown acting on the cut face.

\[ \begin{aligned} &\sum F_y=33{~kips}-V_J=0 \quad\rightarrow\quad V_J=33{~kips} \\ &\sum M_J=-33{~kips}*2{~ft}+M_J=0 \quad\rightarrow\quad M_J=66{~kip}\cdot{ft} \end{aligned} \]

Section K

To find the internal shear, sum forces in the y-direction. To find the internal moment, sum moments at point K.

A beam segment from point A to point K is shown. Point A on the far left has a pinned support with an upward vertical reaction force labeled 33 kips. A vertical downward force of 40 kips is applied 4 feet to the right of point A. The total horizontal distance from point A to point K is 10 feet. At point K, a vertical dashed line marks the cut, where a downward internal shear force V sub K and a counterclockwise internal moment M sub K are shown acting on the cut face.

\[ \begin{aligned} &\sum F_y=33{~kips}-40{~kips}-V_k=0 \quad\rightarrow\quad V_k=-7{~kips} \\ &\sum M_k=-(33{~kips}*10{~ft})+(40{~kips}*6{ft})+M_k \quad\rightarrow\quad M_k=90{~kip}\cdot{ft} \end{aligned} \]

Section L

To find the internal shear, sum forces in the y-direction. To find the internal moment, sum moments at point L.

A beam segment from point A to point L is shown. Point A on the far left has a pinned support with an upward vertical reaction force labeled 33 kips. Two vertical downward forces are applied: 40 kips located 4 feet from A, and 10 kips located 1 foot left of point L. The total horizontal distance from point A to point L is 19 feet. At point L, a vertical dashed line marks the cut, where a downward internal shear force V sub L and a counterclockwise internal moment M sub L are shown acting on the cut face.

\[ \begin{aligned} &\sum F_y=33{~kips}-40{~kips}-10{~kips}-V_L=0 \quad\rightarrow\quad V_L=-17{~kips} \\ &\sum M_L=-(33{~kips}*19{~ft})+(40{~kips}*15{~ft})+(10{~kips}*1{ft})+M_L=0 \quad\rightarrow\quad M_L=17{~kip}\cdot{ft} \end{aligned} \]

Observe that the internal forces vary at different points along the length of the beam. This method of finding the internal stresses is convenient when the loading is simple or when you know a specific point along the length of the beam. However, as the loading becomes more complex, consider one of the methods outlined in the following sections.

7.2 Relationship Between Load, Shear, and Moment

Click to expand

There is a relationship between loading, shear, and moment—and as shown later in this text, slope and deflection—in a beam. Consider the beam in Figure 7.3, which is subjected to a distributed load, w per unit length.

A beam AB is shown with a variable distributed load w applied along its entire length. Point A on the left end has a pinned support, and point B on the right end has a roller support. Along the beam, a small shaded portion is highlighted; the distance from point A to the start of the shaded portion is labeled x, and the width of the shaded portion is labeled Δx. Below the beam, a free body diagram of this differential element Δx is shown. On the left face of the element, an internal shear force V acts upward and an internal moment M acts clockwise. On the right face, the internal shear force is labeled V+ΔV downward, and the internal moment is labeled M+ΔM counterclockwise. A vertical distributed force ΔF=wΔx acts downward across the top of the element.
Figure 7.3: Small segment of a beam subjected to an arbitrary distributed load

Now look at a small section from that beam that has a width of Δx, shown below. The distributed load has been repalced with a resultant force ΔF (this is indicated by a dashed arrow in the FBD).

Since both sides of the beam have been cut, replace each cut with internal shear and moment forces assuming the positive sign convention established earlier in this chapter.

7.2.1 Relationship Between Load and Shear

This FBD is in static equilibrium, so we can use the equilibrium equation to sum forces in the y direction and set it equal to zero.

\[ \sum F_y=V-\Delta F-(V+\Delta V)=0 \\ \]

\[ \boxed{\Delta V=\Delta F} \tag{7.1}\]

Or \[ \Delta V=w\Delta x \]

Dividing both sides by Δx and then letting Δx approach zero produces

\[ \frac{\Delta V}{\Delta x}=\frac{d V}{d x}=w \]

We then rearrange this by multiplying both sides of the equation by dx.

\[ d V=w d x \]

Now we can integrate between any two points A and B on the beam.

\[ \boxed{\underbrace{\Delta V}_{\substack{\text{change in} \\ \text{shear}}}=\int\underbrace{w d x}_{\substack{\text{area under} \\ \text {loading curve}}}} \tag{7.2}\]

This equation is valid for distributed loads, but not when there is a discontinuity in the shear diagram that is caused by concentrated loads. This relationship should be used only between concentrated loads.

7.2.2 Relationship Between Shear and Moment

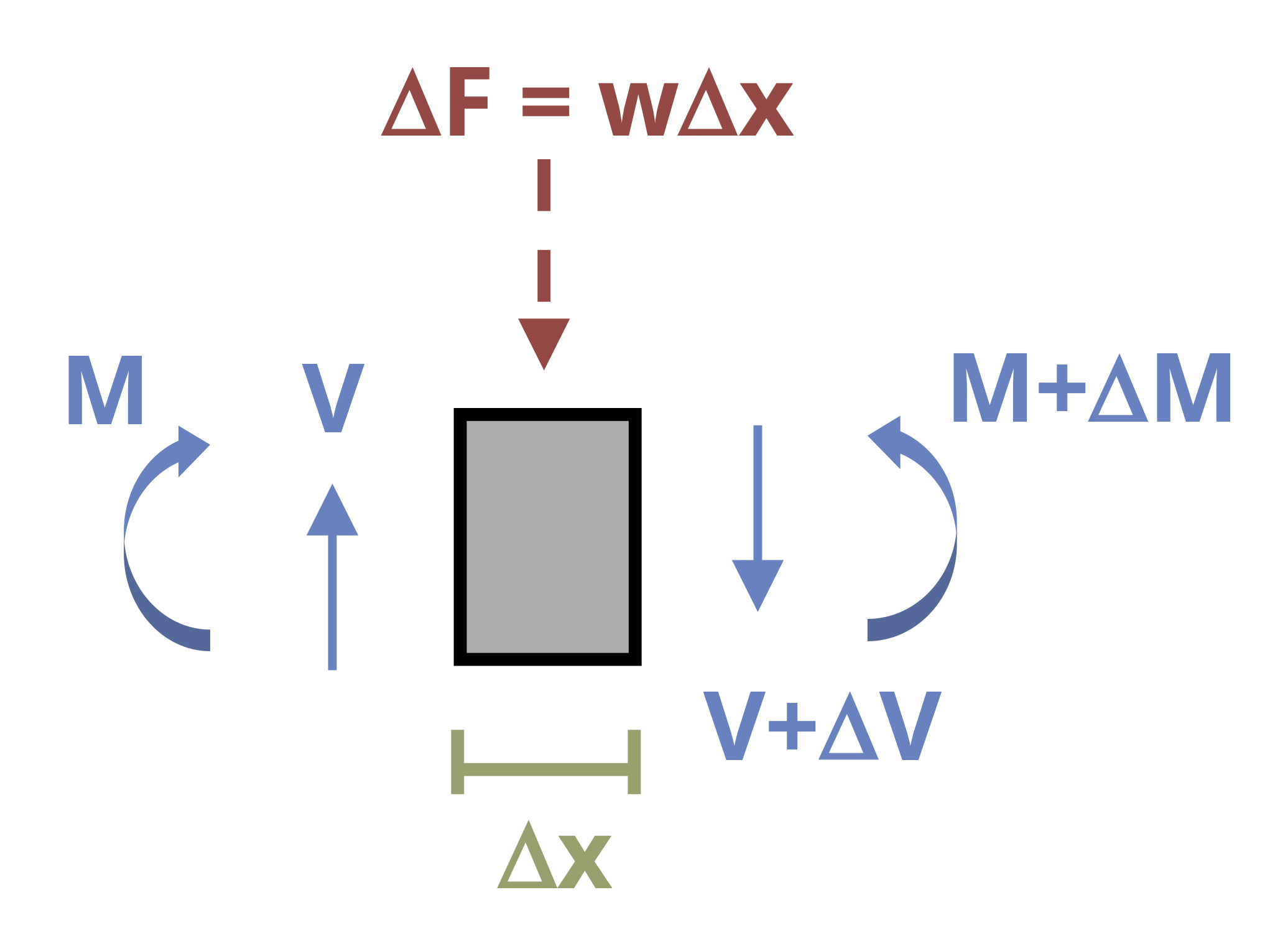
A free body diagram of a differential beam element with width Δx is shown. A small rectangular segment is centered, with a downward distributed force labeled ΔF=wΔx acting on its top. On the left face, an internal shear force V acts upward and an internal moment M acts clockwise. On the right face, an internal shear force V+ΔV acts downward and an internal moment M+ΔM acts counterclockwise. The width of the element is labeled Δx beneath the rectangle.
Figure 7.4: Free body diagram of a small segment of a beam subjected to an arbitrary distributed load

Let’s return to the FBD of the small section of the beam subjected to a distributed load. This segment is shown in Figure 7.4. We can apply another static equilibrium equation, summing moments about point C.

\[ \begin{aligned} \sum M_c=0 & =-M-V(\Delta x)+\Delta F\left(\frac{1}{2} \Delta x\right)+(M+\Delta M) \\ \Delta M & =M+V \Delta x-(w \Delta x)\left(\frac{1}{2} \Delta x\right)-M \\ \Delta M & =V \Delta x-\frac{1}{2} w \Delta x^2 \end{aligned} \]

Dividing both sides by Δx and then letting Δx approach zero yields

\[ \boxed{\underbrace{\frac{\Delta M}{\Delta x}}_{\text { Slope of moment diagram}}=\underbrace{V}_{\text {shear }}} \tag{7.3}\]

Then we rearrange this by multiplying both sides of the equation by dx.

\[ d M=V d x \]

Now it is possible to integrate between any two points A and B on the beam.

\[ \boxed{\underbrace{\Delta M}_{\text {Change in moment}}=\underbrace{\int V d x}_{\text {Area under shear diagram }}} \tag{7.4}\]

This equation is invalid at points where a concentrated force or concentrated moment occurs. These concentrated loads cause discontinuities in the moment diagram.

7.2.3 Using Calculus Knowledge to Build Shear and Moment Diagrams

In a basic sense, the relationship between load, shear, and moment can be described as in Figure 7.5.

A vertical relationship chart is shown with three terms aligned in the center: "Load" at the top, "Shear" in the middle, and "Moment" at the bottom. A thick black downward arrow labeled "Integrate" is positioned to the left, indicating that integrating moves from Load to Shear to Moment. A thick black upward arrow labeled "Derivate" is positioned to the right, indicating that differentiating moves from Moment to Shear to Load.
Figure 7.5: Relationship between load, shear, and moment

Combine these relationships with what you know about derivatives and integrals from your calculus course. Here are some items of note:

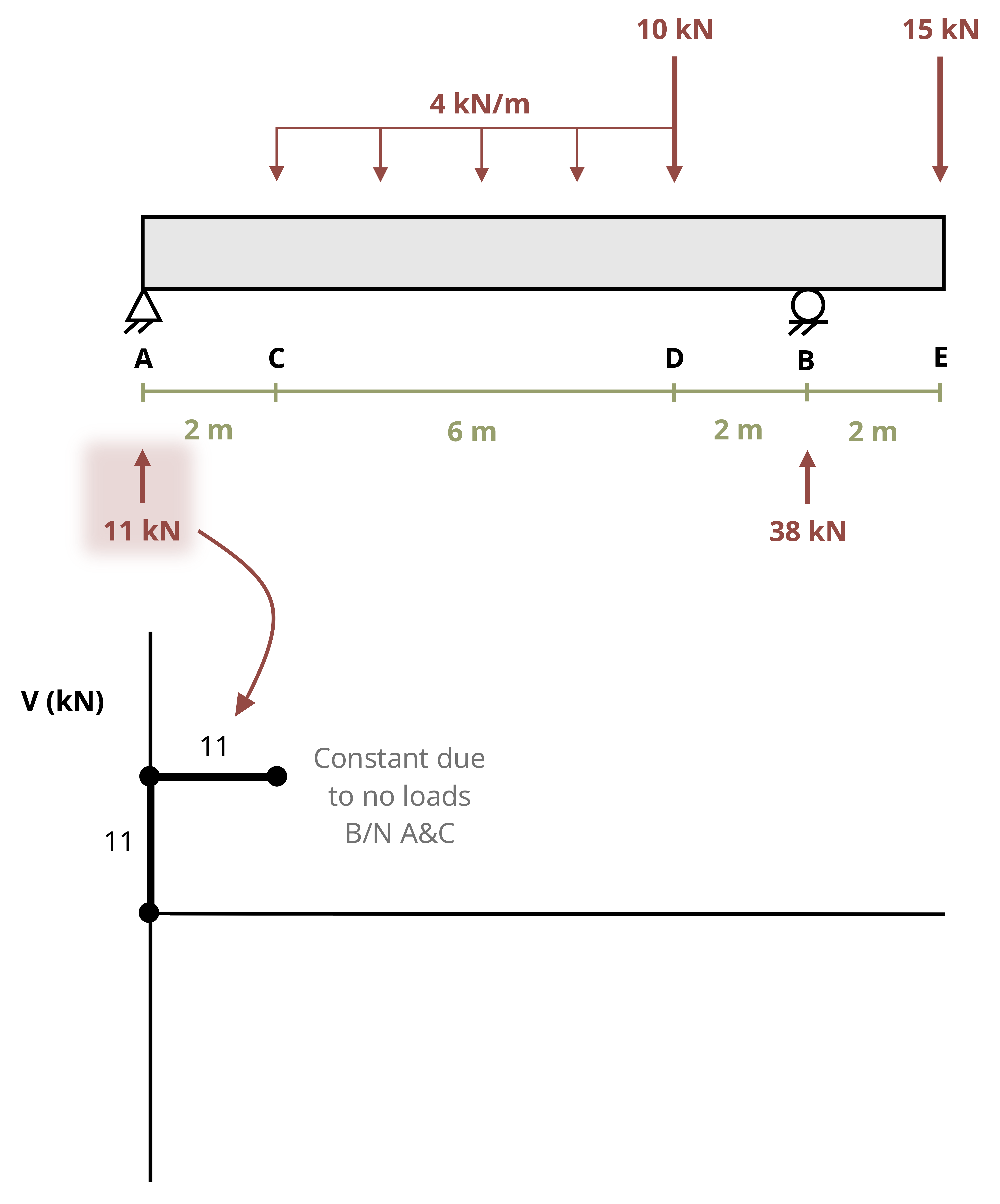
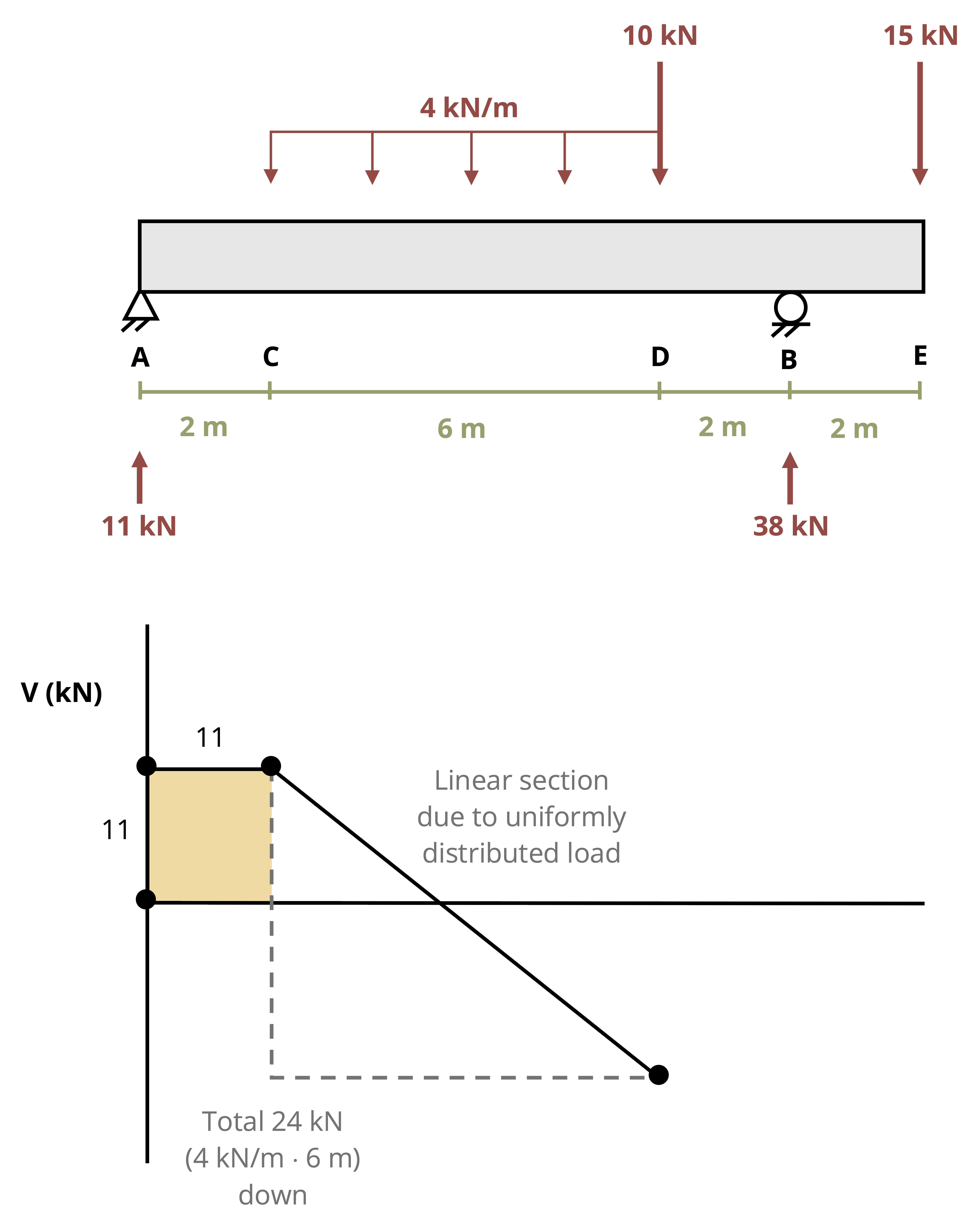
  • The slope of the shear diagram is equal to the sign and magnitude of the distributed load. If there is no load on a section of the beam, then the slope of the shear diagram is zero.

  • Similarly, the slope of the moment diagram at any point is the derivative of the moment function evaluated at that point. This is equal to the sign and magnitude of the shear at that point.

  • The area under the distributed load between two points is equal to the change in the shear between those same two points.

  • The area under the shear diagram between two points is equal to the change in the moment between those same two points.

  • The maximum moment occurs where its derivative (shear) is equal to zero.

  • At the points of concentrated forces, the shear diagram jumps up or down depending on the direction of the force. If the force is up, then the shear diagram will jump up, and if the force is down, the shear diagram will drop down.

  • At the points of concentrated moments, the moment diagram jumps up or down depending on the direction of the rotation. If the concentrated moment is clockwise, the moment diagram will jump up, and if counterclockwise, it will drop down. This “opposite” direction effect for the internal bending moment is the reaction to the applied moment to stay consistent with the established sign convention. The shear diagram remains unaffected.

  • If the load can be represented with a polynomial, then we can easily predict the degree of the subsequent shear and moment functions. For example, if the load is a uniformly distributed load (constant), the shear will be a linear function (n + 1) and the moment will be a parabola (n + 2).

Use all you know about calculus and the relationships between functions when you derive and integrate to build, check, and analyze shear and moment diagrams.

7.3 Determining Equations by Equilibrium

Click to expand

The relationship between load, shear, and moment allows us to build complete shear and moment diagrams using a few different methods. We’ll explore two of them: an equilibrium method and a graphical method.

In Section 7.1 we found the internal shear force and bending moment at specific points in the beam by cutting a cross-section at a given point and using equilibrium. The method in this section is similar, but instead of cutting a cross-section at a specific point, we’ll cut a cross-section at distance x from the left end of the beam. We’ll draw an FBD and determine the internal shear force (V) and bending moment (M) as before, but this time the resulting equations for V and M will be functions of distance x.

To draw the diagrams, we can solve this equation at two values of x. It is often simplest to solve when x = 0 and when x = L, the length of the beam. These are two points we can then connect on our diagram. The diagram’s shape depends on the highest power of x that appears in the equation.

  • For x0 we obtain a flat horizontal line.

  • For x1 we obtain a straight diagonal line.

  • For x2 we obtain a curved line.

  • For x3 we obtain a cubic curve.

If two points are insufficient to determine the exact shape of the curve, simply solve the equations at a third point (e.g., where x = L/2). We can solve the equations at as many points as necessary, but two or three points, along with knowledge of the general shape of the line, are typically sufficient. The equations found using this method are valid as long as the external loading doesn’t change.

Cases where the external loading does change require us to determine a new set of equations each time the loading changes. This includes any time a distributed load begins or ends, and both sides of a concentrated force or couple. In each region of load, we will cut a cross-section at distance x and determine equations for V and M that are valid for that region. We can then solve each equation at values of x at the start and end of their valid region and build up the complete shear force and bending moment diagrams.

Example 7.2 illustrates this method for a simply supported beam, and Example 7.3 for a cantilever beam.

Example 7.2  

Draw the shear force and bending moment diagrams for the beam shown.

A simply supported beam AB is shown. Point A on the left end has a pinned support, and point B on the right end has a roller support. The beam spans a total of 10 feet. A uniformly distributed load of 4 kips per foot is applied from point A to point C, which is 6 feet from A. Additionally, a concentrated vertical downward force of 18 kips is applied at point D, which is 8 feet from A and 2 feet from B. Points C and D divide the beam into segments: AC is 6 feet, CD is 2 feet, and DB is 2 feet.

The first step is to draw an FBD of the beam, being sure to change the supports to the correct external reaction forces as shown.

A simply supported beam AB is shown with a total span of 10 feet. Point A on the left end is a pinned support with reaction forces labeled A sub x (horizontal, rightward) and A sub y (vertical, upward). Point B on the right end is a roller support with a vertical reaction force labeled B sub y (upward). A uniformly distributed load of 4 kips per foot is applied across the first 6 feet of the beam, from point A to point C. Additionally, a concentrated vertical downward force of 18 kips is applied at point D, which is located 8 feet from point A and 2 feet from point B. The beam is divided into three labeled segments: AC (6 feet), CD (2 feet), and DB (2 feet).

We then use static equilibrium equations to solve for the magnitude of the support reactions.

\[ \begin{aligned} &\sum F_x=A_x=0 \\ &\sum M_A=-4\frac{kips}{ft}*6{~ft}*3{~ft}-18{~kips}*8{~ft}+B_y*10{~ft}=0 \quad\rightarrow\quad B_y =21.6{~kips} \\ &\sum F_y=A_y-4\frac{kips}{ft}*6{~ft}-18{~kips}+21.6{~kips}=0 \quad\rightarrow\quad A_y =20.4{~kips} \end{aligned} \]

A simply supported beam AB with a total span of 10 feet is shown. Point A on the far left is a pinned support with reaction forces A sub x (horizontal, rightward) and A sub y (vertical, upward). Point B on the far right is a roller support with a vertical reaction force B sub y (upward). A uniformly distributed load of 4 kips per foot is applied from point A to point C, covering the first 6 feet. A concentrated vertical downward force of 18 kips is applied at point D, which is 8 feet from point A. Three vertical dashed lines represent cut sections along the beam: one located 3 feet from point A, the second 7 feet from point A, and the third 9 feet from point A. The beam is divided into segments labeled AC (6 feet), CD (2 feet), and DB (2 feet).

Next we cut a cross-section within the loading region concerned. When choosing sections, be sure to cut within the uniform load and between loads and reactions. For this example, here we must cut three sections to create the complete shear and moment diagram. These sections are depicted with the green lines. Then the equilibrium equations are used to find the internal shear force as a function of x, V(x).

Section between A and C

A segment of a beam is shown extending from point A to a cut section at distance x from A. A uniformly distributed load of 4 kips per foot acts downward along the entire visible length of the beam. At point A, an upward reaction force labeled 20.4 kips is applied. At the cut face on the right, a downward internal shear force V and a counterclockwise internal moment M are shown. The horizontal distance from point A to the cut is labeled x.

\[ \begin{aligned} &\sum F_y=20.4-4(x) -V=0 \quad\rightarrow\quad V(x)=-4 x+20.4 \\ &\sum M_0=-20.4(x)+4(x)\left(\frac{x}{2}\right)+M=0 \quad\rightarrow\quad M(x)=-2 x^2+20.4 x \\ \end{aligned} \]

Note that you can easily check the statics because V(x) is the derivative of M(x). For polynomials, this is a quick test to see if the equations make sense.

A simply supported beam AB with a total span of 10 feet is shown at the top, supported by a pin at point A and a roller at point B. A uniformly distributed load of 4 kips per foot is applied from point A to point C (a distance of 6 feet), and a concentrated vertical downward force of 18 kips is applied at point D, which is 8 feet from point A. The beam is divided into segments: AC (6 ft), CD (2 ft), and DB (2 ft). Reaction forces are shown: A sub x (horizontal, leftward) and A sub y (vertical, upward) at A, and B sub y (vertical, upward) at B. Below the beam diagram, the shear force diagram (V) shows a linear decrease from 20.4 kips at A due to the distributed load, crossing zero at point C, then dropping sharply at point D due to the point load, and reaching a negative value just before point B. Below that, the bending moment diagram (M) starts at zero at point A, curves upward to a peak between points C and D, reaching a maximum of 50.4 kip-feet, and then drops steeply at point D before returning to zero at point B.

We plot the V(x) and M(x) equations on an axis from x = 0 to x = 6 ft. Solving the equations at these points yields

\[ \begin{aligned} &V(0)=-4(0)+20.4=20.4{~kips} \\ &V(6)=-4(6)+20.4=-3.6{~kips} \\ &M(0)=-2(0)^2+20.4(0)=0 \\ &M(6)=-2(6)^2+20.4(6)=50.4{~kip}\cdot{ft} \end{aligned} \]

Note that the shear diagram is drawn directly below the beam, and the moment diagram directly below the shear. These three—load, shear, and moment—share the same x-axis, whereas the vertical axes for the shear (V) and moment (M) diagrams have different units and possibly different scales.

Drawing the shear and moment diagrams directly below the beam is good practice so that you can get a complete picture of what is going on along the length of the beam.

Section between C and D

A segment of a simply supported beam is shown from point A to an arbitrary point C, a distance x from A, within the uniformly distributed load region. The distributed load is 4 kips per foot applied across the full 6-foot segment from A to C. Point A on the left has a pinned support with horizontal reaction A sub x (leftward) and vertical reaction A sub y (upward). At the cut section on the right at point C, a downward internal shear force V and a counterclockwise internal moment M are shown. The horizontal distance from A to C is labeled x.

\[ \begin{aligned} \sum &F_y=20.4-4(6)-V=0 \quad\rightarrow\quad V(x)=-3.6 \\ \sum &M_0=-20.4(x)+4(6)(x-3)+M=0 \\ &M(x)=+20.4 x-24 x+72 \\ &M(x)=-3.6 x+72 \\ \end{aligned} \]

The top diagram shows a simply supported beam AB with a span of 10 feet. Point A on the left has a pinned support with reaction forces A sub x (horizontal, leftward) and A sub y (vertical, upward), and point B on the right has a roller support with a vertical reaction force B sub y (upward). A uniformly distributed load of 4 kips per foot is applied over the 6-foot segment from A to point C, and a concentrated vertical downward load of 18 kips is applied at point D, which is 8 feet from A. Below the beam diagram are shear force and bending moment diagrams. The shear force diagram (V) starts at 20.4 kips and decreases linearly due to the distributed load, crosses zero at point C, then drops sharply at point D and remains constant until point B. The bending moment diagram (M) starts at zero at point A, curves upward to a peak between C and D, then decreases linearly and reaches a value of 50.4 kip-feet at point D before dropping to zero at point B.

We then add the section from C to D using the V(x) and M(x) equations. Notice that since there are no applied loads on the beam from C to D, the shear diagram remains constant. This means the moment diagram is linear between x = 6 and x = 8 ft.

\[ \begin{aligned} &V(6)=-3.6{~kips} \\ &M(6)=-3.6(6)+72=50.4{~kip}\cdot{ft} \\ &V(8)=-3.6 {kips} \\ &M(8)=-3.6(8)+72=43.2{~kip}\cdot{ft} \\ \end{aligned} \]

Section between D and B

A segment of a simply supported beam is shown from point A to an arbitrary point beyond D, labeled with a variable distance x. Point A has a pinned support with horizontal reaction force A sub x (leftward) and vertical reaction force A sub y (upward). A uniformly distributed load of 4 kips per foot is applied from A to point C (6 feet), and a concentrated vertical downward force of 18 kips is applied at point D (8 feet from A). At the right cut face, located a distance x from point A, a downward internal shear force V and a counterclockwise internal moment M are shown. The beam is divided into segments: AC (6 ft), CD (2 ft), and the remaining segment is labeled with the variable x.

\[ \begin{aligned} \sum &F_y = 20.4-4(6)-18-V=0 \quad\rightarrow\quad V(x) =-21.6 \\ \sum &M_0 =-20.4(x)+4(6)(x-3)+18(x-8)+M=0 \\ & M(x) =20.4 x-24 x+72-18 x+144 \\ &M(x) =-21.6 x+216 \end{aligned} \]

A simply supported beam AB with a total span of 10 feet is shown at the top. Point A has a pinned support with reaction forces A sub x (horizontal, leftward) and A sub y (vertical, upward), while point B has a roller support with vertical reaction force B sub y (upward). A uniformly distributed load of 4 kips per foot is applied over the first 6 feet of the beam from point A to point C. A concentrated vertical downward force of 18 kips is applied at point D, located 8 feet from point A. The beam is divided into segments AC (6 ft), CD (2 ft), and DB (2 ft). Below the beam diagram is the shear force diagram (V), which starts at 20.4 kips, decreases linearly to zero at point C, and continues downward to –3.6 kips at point D. It drops sharply at D to –21.6 kips and remains constant until point B. The bending moment diagram (M) is shown beneath the shear diagram. It starts at zero at point A, curves upward to a maximum of 50.4 kip-feet between points C and D, then decreases linearly to 43.2 kip-feet at point D, and drops back to zero at point B.

Finally, we graph the V(x) and M(x) equations obtained from point D to point B (x = 8 to x = 10 ft).

\[ \begin{aligned} &V(8)=-21.6{~kips} \\ &M(8)=-21.6(8)+216=43.2{~kip}\cdot{ft} \\ &V(10)=-21.6{~kips} \\ &M(10)=-21.6(10)+216=0 \\ \end{aligned} \]

You now have complete shear and moment diagrams. Be sure to label the axes, including units, and all pertinent values.

These diagrams are used in the design of the beam and its components.

A simply supported beam AB is shown with a total span of 10 feet. The beam has a pinned support at point A and a roller support at point B. A uniformly distributed load of 4 kips per foot is applied across the first 6 feet from point A to point C, and a concentrated vertical downward force of 18 kips is applied at point D, located 8 feet from point A. The beam is divided into three segments: AC (6 ft), CD (2 ft), and DB (2 ft). A dashed line beneath the beam represents the deflected shape due to loading, curving downward between supports and indicating maximum deflection near the middle of the span.

Note that in this example, the entire length of the beam is subjected to positive moment. According to the sign convention at the beginning of this chapter, remember, a positive moment indicates a concave up behavior. Given the beam and the external loads, this makes sense, for the beam will want to bend concave up between supports, as the figure shows.

Example 7.3  

Draw the shear force and bending moment diagrams for the beam shown.

A horizontal rectangular bar fixed at the right end. The bar spans points A (leftmost end) and B (rightmost end) and is 10 meters in length. The bar carries a triangular distributed load that increases linearly from zero on the left to a maximum 4 kilonewtons per meter on the right. The load is shown with red arrows and a triangular profile above the beam.

The first step is to draw an FBD of the beam, being sure to change the supports to the correct external reaction forces.

Same figure as above. This figure includes, on the right hand side, an arrow pointing up labaled B sub y, an arrow poiting right labeled B sub x, and an internal bending moment labeled M sub B acts clockwise.

We then use static equilibrium equations to solve for the magnitude of the support reactions.

\[ \begin{aligned} &\Sigma F_x=B_x=0 \\ &\Sigma F_y = -\frac{1}{2}(10~m)\left(4~\frac{kN}{m}\right) + B_y=0 \quad\rightarrow\quad B_y=20~kN \\ &\Sigma M_B=\frac{1}{2}(10~m)\left(4~\frac{kN}{m}\right)\left(\frac{10~m}{3}\right)-M_B=0 \quad\rightarrow\quad M_B=66.7 kN \cdot m \end{aligned} \]

Next we cut a cross-section within the loading region concerned. For this example, we cut one section between A and B to create the complete shear force and bending moment diagram. This section is depicted with the dashed line. Then equilibrium equations are used to find the internal shear force as a function of x, V(x).

Same figure as above. This figure includes a vertical dashed line that splits the 10 meter beam in half.

Section between A and B

Same rectangular bar as described previously. The bar is cut before the fixed support on the right, creating a segment of the original bar. The bar carries a triangular distributed load. The intensity increases linearly from zero at the left to an arbitrary intensity at the cut. At the cut, shown by a vertical dashed line, the internal shear force V acts downward and the internal bending moment M acts counterclockwise.

\[ \Sigma F_y=-V-\frac{1}{2}(x)\left(\frac{4}{10}x\right)=0 \\ V(x)=-\frac{1}{5}x^2 \\ \Sigma M=\frac{1}{2}(x)\left(\frac{4}{10}\right)\left(\frac{1}{3}x\right)+M=0\\ M(x) = -\frac{1}{15}x^3 \]

Note that you can easily check the statics because V(x) is the derivative of M(x). For polynomials, this is a quick test to see if the equations make sense.

We plot the V(x) and M(x) equations on an axis from x = 0 to x = 10 m. Notice how the shear diagram is drawn directly below the beam, and the moment diagram directly below the shear. These three—load, shear, and moment—share the same x-axis, whereas the vertical axes for the shear (V) and moment (M) diagrams have different units and possibly different scales.

Drawing the shear and moment diagrams directly below the beam is good practice so that you can get a complete picture of what is going on along the length of the beam.

Three stacked diagrams. Top: A horizontal rectangular bar fixed at the right end. The bar spans points A (leftmost end) and B (rightmost end) and is 10 meters in length. The bar carries a triangular distributed load that increases linearly from zero on the left to a maximum 4 kilonewtons per meter on the right. The load is shown with red arrows and a triangular profile above the beam. Middle: A shear force diagram begins at zero kilonewtons, decreases parabolically (concave down) to -20 kilonewtons at the support. Bottom: A bending moment diagram follows the same shape as the shear force diagram, starting at zero kilonewton meters and decreasing parabolically (concave down) to -66.7 kilonewton meters at the support.

See that the shear diagram starts at zero, then at X = 10 m, V(10) = -20 kN. The reaction calculated was 20 kN going up, so adding that reaction closes the shear diagram.

Similarly, the moment diagram is the graph of the cubic equation from x = 0 to x = 10. M(10) = -66.7 kN·m is the same as the reaction calculated to close the moment diagram.

Note that in this example the entire length of the beam is subjected to negative moment. According to the sign convention presented at the beginning of this chapter, remember, a negative moment indicates a concave down behavior. Given the beam and the external loads, this makes sense because the beam will want to bend concave down, as shown in the figure.

A horizontal rectangular bar fixed at the right end. The bar spans points A (leftmost end) and B (rightmost end) and is 10 meters in length. The bar carries a triangular distributed load that increases linearly from zero on the left to a maximum 4 kilonewtons per meter on the right. The load is shown with red arrows and a triangular profile above the beam. A dashed bar beneath the beam represents the deflected shape due to loading, curving downward on the left while remaining fixed at the right, indicating maximum deflection near the left of the span.

WarningStep-by-Step: Shear Force and Bending Moment Diagrams (equilibrium method)

  1. Use equilibrium to determine the reaction loads at any supports.

  2. Identify the distinct regions of external loading and cut a cross-section within each region.

  3. Draw an FBD of the left side of the first cut, which should be made at distance x1. Use equilibrium to determine equations for the internal shear force (V) and bending moment (M) as functions of x1.

  4. Repeat step 3 for each loading region and develop equations for V and M that are valid in each region.

  5. Plot each set of equations on axes of V(x) and M(x). Each equation is valid only in the region where it was developed. Solve each equation at the start and end points of its region and then connect the points with an appropriate line, according to the highest power of x that appears in the equation.

7.4 Graphical Method Shear Force and Bending Moment Diagrams

Click to expand

An alternative, often faster method for drawing shear force and bending moment diagrams is the graphical method. This approach leverages the relationships between load, shear force, and bending moment, allowing us to derive one diagram from another.

Specifically, Section 7.2 showed that \(\frac{dV}{dx}=w\) and \(\frac{dM}{dx}=V\). That is, the slope of the shear force diagram at any point equals the applied distributed load at that point, and the slope of the bending moment diagram at any point equals the shear force at that point.

Further, any applied concentrated force causes a jump in the shear diagram (e.g., an upward force results in an upward jump). Any applied couples causes a jump in the bending moment diagram (e.g., a clockwise moment causes an upward jump). Thus the shape of the shear force diagram is based on the applied loads, and the shape of the bending moment diagram is based on the shear force diagram.

Finally, Equation 7.2 also showed that the change in shear force between any two points is equal to the area under the distributed load between those same two points. Evident from Equation 7.4 is that the change in bending moment between any two points is equal to the area underneath the shear force diagram between those two points. This allows us to add numbers to the diagrams and determine the value of the shear force and bending moment at key points.

When the loading is relatively simple, consisting of concentrated forces, concentrated moments, and uniformly distributed loads, we can use geometry to find the area of the load and shear diagrams since the shapes are simple. Example 7.4 and Example 7.5 illustrate this method.

Example 7.4  

Draw the shear force and bending moment diagrams for the beam shown.

Simply supported beam subjected to distributed and point loads. In the top diagram, a 12-meter-long horizontal beam spans between point A on the left, which has a triangular pin support, and point B on the right, which has a circular roller support. A uniformly distributed load of 4 kN/m is applied over the central 6 meters of the beam, starting 2 meters from A and ending 2 meters before B. A concentrated downward force of 10 kN is located 8 meters from A, and another concentrated downward force of 15 kN is applied 12 meters from A.

The same beam is shown with reaction forces: a rightward horizontal force labeled A sub x and an upward vertical force labeled A sub y at point A, and an upward vertical reaction force labeled B sub y at point B.

The first step is to draw an FBD of the beam, being sure to change the supports to the correct external reaction forces, as shown below.

Then use static equilibrium equations to solve for the magnitude of the support reactions.

\[ \begin{aligned} &\sum F_x=A_x=0 \\ &\sum M_A=-4\frac{kN}{m}(6{~m})(5{~m})-10{~kN}(8{~m})+B_y(10{~m})-15{~kN}(12{~m})=0 \quad\rightarrow\quad B_y =38{~kN} \\ &\sum F_y=A_y-4\frac{kN}{m}(6{~m})-10{~kN}-15{~kN}+38{~kN} \quad\rightarrow\quad A_y =11{~kN} \end{aligned} \]

Now that the external forces are known, build the shear diagram. Start at the leftmost point of the beam, point A.

Beginning of a shear force analysis for a simply supported beam subjected to distributed and point loads. The beam spans from point A to point E, with intermediate points labeled C, D, and B. The beam is supported by a pin at A and a roller at B. A uniformly distributed load of 4 kN/m is applied between points C and D, a 10 kN downward point load is applied at point D (8 meters from A), and a 15 kN downward point load is applied at point E (12 meters from A). Reaction forces are shown: an upward vertical force of 11 kN at A and an upward vertical force of 38 kN at B. Below the beam, the corresponding shear force diagram is shown for the segment between A and C. It begins at +11 kN and remains constant in this interval, indicating no applied loads between points A and C. A label notes this constancy with the text “Constant due to no loads B/N A & C.”

The first force encountered is at point A, the reaction force of 11 kN. The force is going up, so do that same thing on the shear diagram.

From that point, look at the beam and note that no forces are acting between points A and C. This indicates the shear diagram will remain constant at 11 kN.

Simply supported beam subjected to a uniformly distributed load of 4 kN/m across a 6-meter span from point C to point D, a 10 kN downward force at point D (8 meters from point A), and a 15 kN downward force at point E (12 meters from point A). Support reactions are shown as an 11 kN upward force at point A and a 38 kN upward force at point B. Below the beam is the shear force diagram, which starts at +11 kN, remains constant between points A and C, then decreases linearly to –13 kN due to the distributed load across CD. The linear drop is annotated as “Linear section due to uniformly distributed load,” with a boxed area indicating a total drop of 24 kN.

The 4 kN/m uniformly distributed load starts at point C and goes for 6 m until point D. The force is going down for a total of 24 kN (4 kN/m·6 m). Since the load is constant from point C to D, the shear will be linear between those points. The slope of the shear diagram will be -4 and over those 6 m will decrease the total of 24 kN.

Simply supported beam subjected to a 4 kN/m uniformly distributed load from point C to D (6 meters), a 10 kN downward point load at point D (8 meters from A), and a 15 kN downward point load at point E (12 meters from A). Vertical support reactions are shown as an 11 kN upward force at A and a 38 kN upward force at B. Below the beam, the shear force diagram begins at +11 kN at point A, remains constant to point C, then linearly decreases due to the distributed load to –13 kN at point D. At point D, the shear diagram shows a vertical drop of 10 kN from –13 kN to –23 kN, labeled “Jump down 10 kN to match load.” From point D to B, the diagram remains constant at –23 kN, labeled “Constant due to no loads B/N D & B.”

At point D there is a concentrated 10 kN load going down. On the shear diagram, this load will be represented by a discontinuity, jumping down by 10 kN to -23 kN.

From that point look at the beam and note that no forces are acting between points D and B. This indicates the shear diagram will remain constant at -23 kN.

Simply supported beam and its corresponding shear force diagram. The beam is supported at point A on the left and point B, located 10 meters from A, with a total beam length of 14 meters extending to point E. The beam includes a 4 kN/m uniformly distributed load between points C and D (from 2 m to 8 m), a 10 kN downward point load at D (8 m from A), and a 15 kN downward point load at point E (14 m from A). The reaction forces are 11 kN upward at A and 38 kN upward at B. Below the beam, the shear diagram starts at +11 kN at A, remains constant to C, then decreases linearly to –13 kN at D due to the distributed load. It then drops vertically to –23 kN at D due to the 10 kN point load. At B, the shear force jumps up 38 kN to +15 kN and remains constant to E, labeled “Constant due to no loads B/N B & E.”

At point B, the roller support, there is an external reaction of 38 kN going up. This concentrated force will cause a discontinuity in the shear diagram. From -23 kN add 38 kN to end at 15 kN.

From that point look at the beam and note that no forces are acting between points B and E. This indicates the shear diagram will remain constant at 15 kN.

Simply supported beam and its corresponding shear force diagram. The beam has a pin support at point A and a roller support at point B, with a total length of 14 meters from A to E. It is subjected to a uniformly distributed load of 4 kN/m from 2 meters to 8 meters (C to D), a 10 kN point load at point D (8 meters from A), and a 15 kN point load at point E (14 meters from A). The support reactions are 11 kN upward at A and 38 kN upward at B. Below, the shear diagram starts at +11 kN at A, stays level to point C, then slopes down linearly to –13 kN at point D due to the uniformly distributed load. At D, it drops vertically to –23 kN due to the 10 kN point load. At B, the shear jumps up 38 kN to +15 kN, and finally drops vertically by 15 kN at point E to return to zero, indicating the applied 15 kN downward load. The jump is labeled “Jump down 15 kN to match load.”

At point E see a 15 kN concentrated force going down. This concentrated force will cause a discontinuity in the shear diagram. From 15 kN subtract 15 kN to end back at zero.

The shear diagram should start and end at zero. At the end of the beam the shear diagram “closes,” which means that it ends back at zero. This is a good check that you are on the right track. However, rounding reactions might lead to a slightly off result at the end of your shear diagram.

Now having the shear diagram, you can build the moment diagram. Remember from the previous section that the internal moment is the area under the shear diagram. Because the shear diagram consists of basic shapes (rectangles and triangles), you can use geometry to find these areas.

Beam subjected to a combination of loads and its corresponding shear and moment diagrams. The beam is supported by a pin at point A and a roller at point B. It spans 14 meters and is loaded with a uniformly distributed load of 4 kN/m from point C to D, a 10 kN point load at D (8 meters from A), and a 15 kN point load at E (14 meters from A). Reaction forces are shown as 11 kN upward at A and 38 kN upward at B. The shear diagram starts at +11 kN, remains constant from A to C, and decreases linearly to –13 kN at D due to the uniformly distributed load. It then drops vertically to –23 kN from the 10 kN point load and jumps up to +15 kN at B, before finally dropping to zero at E due to the 15 kN point load. Below, the moment diagram shows a triangular area from A to C, peaking at 22 kN·m, which is labeled as a linear section due to constant shear.

Just as for the shear diagram, start at zero at the leftmost point of the beam, point A. The first section from A to C is a rectangle. Calculate the area under the shear curve to find the change in the internal moment between A and C. Keep in mind the following three things:

  • Magnitude of the change: Magnitude of the change is the area under the curve. The height of the rectangle is 11 kN, and the width is 2 m, so the area is 22 kN·m.

  • Direction of the change: Direction of the change is on the positive side of the shear diagram, which indicates that it will go up from A to C.

  • Shape of the segment: The shear diagram is constant, so the moment diagram will be linear with a slope of 11.

Simply supported beam with a triangular shear diagram and a curved moment diagram below. The beam has a pin at A and a roller at B, with a uniformly distributed load of 4 kN/m over a central 6-meter span, a 10 kN point load at D (8 meters from A), and a 15 kN point load at E (14 meters from A). Reaction forces of 11 kN at A and 38 kN at B are indicated. The shear diagram starts at +11 kN and decreases linearly due to the distributed load, intersecting the axis at approximately 2.75 meters from C. A triangular area from this point to D is highlighted and calculated to be 15.125 kN·m. The moment diagram below starts at zero, rises linearly to 22 kN·m at C, and then curves up to 37.125 kN·m, forming a parabolic segment due to the linearly varying shear.

From point C to D there are two triangles, one that is on the positive side of the shear diagram and the other that is on the negative side.

To calculate the area under the curve, first calculate the distance from point C to where the shear diagram crosses the x-axis.

There are many ways to do this. We illustrate using similar triangles to find this distance. In the figure, we are comparing the larger yellow triangle and the smaller pink triangle, where unknown distance x is the base. To accomplish this we set up the following proportion

\[ \frac{24{~kN}}{6{~m}}=\frac{11{~kN}}{x} \quad \therefore \quad x=2.75 \mathrm{~m} \]

Magnitude of the Change

Magnitude of the change encompasses the area under the curve. The area of the triangle is 15.125 kN·m [A = ½ (2.75 m)(11 kN)]

Direction of the Change

This area is on the positive side of the shear diagram, which indicates it will go up from C to the zero point on the shear diagram. So add the area, 15.125, to the internal moment at point C (22 kN·m) to be at 37.125 kN·m at the point of zero shear.

Shape of the Segment

The shear diagram is linear, so the moment diagram will be parabolic and concave down.

Beam with a pin at A and a roller at B, subject to a uniformly distributed load of 4 kN/m between points C and D (a 6-meter span), a 10 kN point load at D, and a 15 kN point load at E. Support reactions are marked as 11 kN upward at A and 38 kN upward at B. The shear diagram below the beam shows a triangular negative area under the x-axis from the end of the distributed load to point D, calculated as 21.125 kN·m. This area corresponds to the region where the shear is negative. The moment diagram beneath shows a parabolic curve that peaks at 37.125 kN·m and then drops to 16 kN·m, reflecting the subtraction of 21.125 from the earlier peak. The moment shape is parabolic due to the linear variation in shear.

We can now account for the second triangle from C to D.

Magnitude of the Change

Magnitude of the change encompasses the area under the curve. The area of the triangle is

\[ A=\frac{1}{2}*(6-2.75)*13=21.125{~kN\cdot m} \]

Direction of the Change

This area is on the negative side of the shear diagram, which indicates it will go down from the point of zero shear to point D. So subtract the area 21.125 to the internal moment at the zero point (37.125 kN) to be at 16 kN·m at point D.

Shape of the Segment

The shear diagram is linear, so the moment diagram will be parabolic and concave down. The concavity of a parabolic function can be determined by examining whether the shear diagram is increasing or decreasing. In this example, the shear diagram is decreasing between points C and D, so the parabola will be concave down.

The diagram at the top shows a beam supported by a pin at point A and a roller at point B, subjected to a uniformly distributed load of 4 kN/m between points C and D, a 10 kN point load at D, and a 15 kN point load at E. Reaction forces include an 11 kN upward force at A and a 38 kN upward force at B. The shear force diagram beneath the beam reflects these loads, beginning at 11 kN, sloping downward linearly due to the distributed load, stepping down by 10 kN at D, and finally stepping up by 38 kN at B before dropping by 15 kN at E. The final negative rectangular area is labeled with an area of 46 kN·m, located beneath the x-axis. The bending moment diagram at the bottom shows a triangular region rising to 22 kN·m from the initial positive shear, followed by a parabolic peak at 37.125 kN·m due to the linear variation of shear, and ending with a straight-line descent to −30 kN·m, indicating the subtraction of 46 kN·m under constant shear.

We are now able to account for the section from D to B.

Magnitude of the Change

Magnitude of the change encompasses the area under the curve. The height of the rectangle is 23 kN, and the width is 2 m, so the area is 46 kN·m.

Direction of the Change

This area is on the negative side of the shear diagram, which indicates it will go down from D to B. Here subtract the area from the internal moment at D. So calculate 16 - 46 to end at negative 30.

Shape of the Segment

Because the shear diagram is constant, the moment diagram will be linear with a slope of -23.

The diagram at the top shows a simply supported beam with a pin support at point A and a roller support at point B. The beam is subjected to a uniformly distributed load of 4 kN/m between points C and D, a concentrated downward load of 10 kN at point D (8 meters from A), and another concentrated downward load of 15 kN at point E (12 meters from A). The reactions at the supports include an 11 kN upward force at A and a 38 kN upward force at B. Below, the shear diagram begins at 11 kN, remains constant between A and C, then decreases linearly due to the uniformly distributed load from C to D, dropping from 11 to −13 kN. At D, it drops further to −23 kN due to the 10 kN load, then jumps to 15 kN at B due to the support reaction, and finally drops back to 0 kN at E due to the 15 kN load. The bending moment diagram below the shear plot shows a triangular region increasing linearly to 22 kN·m from point A to C, a parabolic peak at 37.125 kN·m resulting from the distributed load from C to D, followed by a curved drop to 16 kN·m at point B, and a final linear decline from 16 kN·m to 0 at point E due to the constant shear in that region.

Finally, we can build our moment diagram from B to E.

Magnitude of the Change

Magnitude of the change encompasses the area under the curve. The height of the rectangle is 15 kN and the width is 2 m, so the area is 30 kN·m.

Direction of the Change

This area is on the positive side of the shear diagram, which indicates it will go up from B to E. Here add the area from the internal moment at B. So calculate (-30 + 30) to end at zero.

Shape of the Segment

The shear diagram is constant, so the moment diagram will be linear with a slope of +15.

At the end of the beam, the moment diagram “closes,” which means it ends back at zero. Moment diagrams must start and end at zero. This is a good check that you are on the right track. However, rounding reactions and areas might lead to a slightly off result at the end of the moment diagram.

The diagram at the top shows a simply supported beam with a triangular support at point A and a roller support at point B. A uniformly distributed load of 4 kN/m spans from point C to point D, a 10 kN concentrated downward force is applied at point D (8 meters from point A), and a 15 kN concentrated downward force is applied at point E (12 meters from point A). The support reactions are an 11 kN upward force at point A and a 38 kN upward force at point B. Below, the shear diagram begins at 11 kN, remains constant between A and C, and then decreases linearly due to the distributed load from C to D, dropping to −13 kN. At D, the shear diagram jumps down to −23 kN due to the 10 kN force, then jumps up to 15 kN at B from the 38 kN reaction, and finally drops to 0 kN at E from the 15 kN load. The bending moment diagram underneath starts at 0, increases linearly to 22 kN·m between A and C, curves upward to a peak of 37.125 kN·m between C and D due to the triangular area of shear, and then curves downward to 16 kN·m at B. From B to E, the moment decreases linearly to 0, completing the diagram.

The final product is shown in the figure above. To have complete shear and moment diagrams you should label your axes, including units, and indicate the pertinent values on each diagram. As mentioned earlier, it’s best to draw these diagrams right below the beam so that seeing what the internal shear and bending moment forces are in relation to a location on the beam is easy.

A simply supported beam is shown with a triangular support at point A and a roller support at point B. The beam spans 12 meters total, divided into segments of 2 meters, 6 meters, 2 meters, and 2 meters. A uniformly distributed load of 4 kN/m spans the middle 6-meter segment, and two concentrated downward forces are applied—10 kN at 8 meters from A (point D), and 15 kN at 12 meters from A (point E). Below the beam is a single continuous blue curve indicating the qualitative shape of the deflected beam under loading. The deflection is shown curving downward between A and D, reaching a maximum displacement near midspan, then curving upward from D to E, indicating a shift in curvature due to applied loads and support reactions.

This example shows that this beam is subjected to both positive and negative moments. Remember that a positive moment indicates concave up bending behavior, and a negative indicates concave down. Given the beam and the external loads, it makes sense that the beam will want to bend concave up between supports in the area of positive moment. The beam will then bend concave down over support B in the area of negative moment, as shown in the figure.

Example 7.5  

Draw the shear force and bending moment diagrams for the beam shown.

A cantilever beam is fixed at the left end at point A and extends horizontally 6 feet to the right. The beam is divided into three segments: AB is 2 feet, BC is 1 foot, and CD is 3 feet. A downward force of 2 kips is applied vertically above point B through an offset vertical extension, and a second downward force of 5 kips is applied directly at point D.

This beam differs a little from other examples in this chapter as the support is a fixed end and includes a force-couple system at point C. Nonetheless, the processes that have been presented here apply in this situation.

A horizontal beam is shown with supports and reaction components at the fixed end A, which include a vertical force A sub y pointing upward, a horizontal force A sub x pointing to the right, and a counterclockwise moment M sub A. A downward force of 2 kips is applied at point C, 3 feet from the fixed end, accompanied by a counterclockwise moment of 2 kip-feet at the same location. An additional downward force of 5 kips is applied at point D, which is 6 feet from point A.

The first step is to draw an FBD of the beam, being sure to change the supports to the correct external reaction forces, as shown to the left. The 2 kips that acts on the arm at point B will cause a force on beam AD at the connection point, C. Additionally, a concentrated moment from this force also acts at point C. The magnitude of this concentrated moment is (2 kips)(1 ft) or 2 k·ft counterclockwise.

We then use static equilibrium equations to solve for the magnitude of the support reactions.

\[ \begin{aligned} &\sum F_x=A x=0 \\ &\sum F_y=A_y-2{~kips}-5{~kips}=0 \quad\rightarrow\quad A_y=7{~kips} \\ &\sum M_A = M_A + 2{~kip\cdot ft} - 2{~kips}(3{~ft}) - 5{~kips}(6{~ft})=0 \quad\rightarrow\quad M_A=34{~kip\cdot ft} \\ \end{aligned} \]

A horizontal beam is shown with the same loading and support configuration as before: a fixed support at A, a downward force of 2 kips with a clockwise moment of 2 kip-feet at C, and a downward force of 5 kips at D. Below the beam is the corresponding shear diagram. The shear diagram begins at 7 kips and remains constant until point C, where it drops vertically to 5 kips due to the 2-kip downward force. It then continues horizontally at 5 kips until point D.

We can now build the shear diagram. Keep in mind that the concentrated moments (at points A and C) do not contribute to the shear diagram.

We start with the vertical reaction at point A. This is going up 7 kips. Then because no loads are on the beam between A and C, the shear diagram remains constant.

The concentrated force at point C is 2 kips down. So we subtract 2 kips from 7 kips. With no loads between points C and D, the shear diagram remains constant at 5 kips.

At point D there is a concentrated load of 5 kips down. This brings the shear diagram to a close at zero.

A beam diagram is shown at the top with a fixed support at A, a 2-kip downward force and a 2 kip-foot clockwise moment at C, and a 5-kip downward force at D. Below the beam is the shear force diagram, starting at 7 kips and dropping to 5 kips at point C, then continuing horizontally to point D. The area under the 7-kip region is shaded dark orange and labeled as 7 × 3 = 21. Below this is the bending moment diagram, starting at -38 kip-feet at point A and increasing linearly to 13 kip-feet at point D. The moment increase is noted as +21 due to the constant 7-kip shear over 3 feet.

We next build the moment diagram with the combination of the area of the shear diagram and the concentrated moments.

We start from zero and go down 34 kip·ft since the reaction at A, MA, is counterclockwise.

Between A and B

Magnitude of the Change

Magnitude of the change encompasses the area under the curve. The height of the rectangle is 7 kips and the width is 3 ft, so the area is 21 kip·ft.

Direction of the Change

This area is on the positive side of the shear diagram, which indicates it will go up from A to C. We add the area from the internal moment at A (-34 + 21 = -13 kip·ft).

Shape of the Segment

The shear diagram is constant, so the moment diagram is linear with a slope of +7 kips/ft.

Horizontal beam fixed at point A, with a vertical downward force of 2 kips applied at point C and 5 kips at point D. A counterclockwise moment of 2 kip-feet is also applied at point C. The shear force diagram below the beam indicates a constant shear of 7 kips from A to C, dropping to 5 kips from C to D. The moment diagram beneath shows a linear increase from negative 38 kip-feet at A to 15 kip-feet at point C, then a sudden vertical drop to 13 kip-feet due to the counterclockwise moment at C. A note on the diagram clarifies the drop by stating “CCW so drop down.”

An applied concentrated moment of 2 kip·ft counterclockwise at point C creates a discontinuity in the moment diagram by dropping down 2 (-13 - 2 = -15 kip·ft).

A beam is shown with a downward force of 2 kips at point C and 5 kips at point D, along with a counterclockwise moment of 2 kip-feet applied at point C. The shear diagram indicates a value of 7 kips from A to C, then drops to 5 kips from C to D. The moment diagram begins at -38 kip-feet at point A, increases linearly to 15 kip-feet at point D, with a sudden drop from 15 to 13 kip-feet at point C due to the counterclockwise moment. The final triangle in the moment diagram reflects an area of 15 kip-feet created by the constant shear of 5 kips over the 3-foot span.

Between C and D

Magnitude of the Change

Magnitude of the change encompasses the area under the curve. The height of the rectangle is 5 kips and the width is 3 ft, so the area is 15 kip·ft.

Direction of the Change

This area is on the positive side of the shear diagram, which indicates it will go up from C to D. Here we add the area from the internal moment at A (-15 + 15 = 0).

Shape of the Segment

The shear diagram is constant, so the moment diagram is linear with a slope of +5 kip/ft.

A beam is subjected to a 2 kip downward force and a 2 kip-foot counterclockwise moment at point C, along with a 5 kip downward force at point D. The shear diagram shows a constant 7 kips from A to C, then drops to 5 kips from C to D. In the moment diagram, the value increases linearly from -38 kip-feet at point A to 13 kip-feet just before point C. At C, a vertical drop to 15 kip-feet occurs due to the counterclockwise moment. From C to D, the moment continues to increase linearly from 15 kip-feet to zero at the end.

The final shear and moment diagram is in the figure to the left. Note that this cantilever structure with downward loads will bend concave down. This indicates that the entire beam will be in negative moment—which is also what our moment diagram indicates.

WarningStep-by-Step: Shear Force and Bending Moment Diagrams (graphical method)

  1. Use equilibrium to determine the reaction loads at any supports.

  2. Use the loading diagram to draw the shear force diagram. Begin at the left end of the beam and move to the right, obeying these rules.

    • A concentrated force causes a discontinuity on the shear diagram. An upwards force causes a jump upward.

    • A distributed load causes a slope on the shear diagram equal to the size of the distributed load. An upward load causes a slope upward.

      • The total change in shear force due to a distributed load is equal to the area underneath the distributed load.

    • Anywhere there are no applied forces, the shear force does not change.

    • The shear force diagram should start and end at zero. If it does not, go back and check for errors.

  3. Once the shear force diagram is complete, use it to draw the bending moment diagram. Begin at the left end of the beam and move to the right, obeying these rules.

    • An applied couple causes a discontinuity on the moment diagram. A clockwise couple causes a jump upward, and a counterclockwise couple causes a jump downward.

    • The slope of the moment diagram at any point is equal to the shear force at that point. As the shear force changes, the slope of the moment diagram will change too.

      • If the shear force is zero, the bending moment will be constant.

      • If the shear force is constant, the slope of the moment diagram will be linear.

      • If the shear force is linear, the slope of the moment diagram will be parabolic.

      • If the shear force is positive, the moment diagram will slope upward.

      • If the shear force is negative, the moment diagram will slope downward.

      • As the magnitude of the shear force increases, the slope of the bending moment diagram becomes steeper.

    • The bending moment diagram should start and end at zero. If it does not, go back and check for errors.

Summary

Click to expand
NoteKey Takeaways

Shear and moment diagrams allow us to calculate and visualize the internal forces of beams. These internal forces are used to calculate stresses and deformations (covered in upcoming chapters). The general procedure for building the shear and moment diagrams is as follows:

  1. Sketch the beam, replacing support conditions with equivalent force(s).
  2. Find the support reactions using equilibrium.
  3. Use the method of equations or geometry or a combination to build the shear diagram directly below your beam sketch.
  4. Use the method of equations or geometry or a combination to build the moment diagram directly below your shear diagram.
  5. Ensure that your diagrams are labeled, including units, and that all pertinent values are indicated.
NoteKey Equations

Relationship between load and shear:

\[ \Delta V=\Delta F \] \[ \underbrace{\Delta v}_{\substack{\text{change in} \\ \text{shear}}}=\int\underbrace{w d x}_{\substack{\text{area under} \\ \text {loading curve}}} \]

Relationship between shear and bending:

\[ d M=V d x \] \[ \underbrace{\Delta M}_{\text {Change in moment}}=\underbrace{\int V d x}_{\text {Area under shear diagram }} \]

References

Click to expand

Figures

All figures in this chapter were created by Kindred Grey in 2025 and released under a CC BY license, except for